
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,若⊙
,若⊙![]() 的圆心在线段
的圆心在线段![]() 上,且⊙
上,且⊙![]() 与
与![]() 都相切,则⊙
都相切,则⊙![]() 的半径是___________.
的半径是___________.

【答案】![]()
【解析】
过O点作OM⊥AC、ON⊥AB,设⊙O半径为R,求出OM=MP=R,根据勾股定理求出BP,OP,求出BO,根据切线长定理求出AN=AM=1+R,求出BN,在Rt△BNO中,根据勾股定理求出即可.
过O点作OM⊥AC、ON⊥AB,
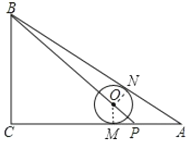
∵⊙O与AB、AC都相切,
∴AN=AM,OM⊥CP,ON⊥AB,
∴∠BNO=∠OMP=90 ![]() ,
,
设⊙O半径为R,
在Rt△ABC中,∠C=90 ![]() ,AC=4,AB=5,由勾股定理得:BC=3,
,AC=4,AB=5,由勾股定理得:BC=3,
∵AP=1,AC=4,
∴CP=41=3=BC,
∴∠CBP=∠CPB=45 ![]() ,
,
∵∠OMP=90 ![]() ,
,
∴∠MOP=45 ![]() =∠OPM,
=∠OPM,
∴OM=MP=R,
在Rt△OMP中,由勾股定理得:PO=![]() R,
R,
在Rt△BCP中,由勾股定理得:BP=3 ![]() ,
,
则BO=3![]()
![]() R,AM=AN=1+R,
R,AM=AN=1+R,
∴BN=BAAN=5(1+R)=4R,
∵在Rt△BNO中,由勾股定理得:BN2+ON2=BO2,
∴(4R)2+R2=(3![]()
![]() R)2,
R)2,
解得:R=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
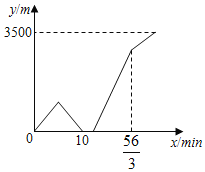
【题目】5月的第二个周日是母亲节,丁丁精心地设计了一份手工礼物送给妈妈.为了尽快完成手工礼物,丁丁骑自行车到位于家正东方向的商店购买材料.丁丁离家5分钟后自行车出现故障,丁丁立即打电话通知在家看报纸的爸爸带上工具箱来帮忙维修(丁丁打电话和爸爸找工具箱的时间忽略不计),同时丁丁以原来一半的速度推着自行车继续走向商店.爸爸接到电话后,立刻出发追赶丁丁,追上丁丁后,爸爸用2分钟的时间修好了自行车,并立刻以原速到位于家正西方500米的公司上班(爸爸换电话的时间忽略不计),丁丁则以原来的骑车速度到达商店.在整个过程中,丁丁和爸爸保持匀速行驶.如图是丁丁、爸爸的距离y(米)与丁丁的出发时间x(分钟)之间的函数图象,则爸爸到达公司时,丁丁距离商店_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b 的图象与反比例函数y=![]() 的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:
的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:
(1)一次函数的解析式;
(2)△AOB的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“双十二购物狂欢节”活动,某零食店推出了甲、乙、丙三类饼干礼包,已知甲、乙、丙三类礼包均由![]() 、
、![]() 、
、![]() 三种饼干搭配而成,每袋礼包的成本均为
三种饼干搭配而成,每袋礼包的成本均为![]() 、
、![]() 、
、![]() 三种饼干成本之和.每袋甲类礼包有5包
三种饼干成本之和.每袋甲类礼包有5包![]() 种饼干、2包
种饼干、2包![]() 种饼干、8包
种饼干、8包![]() 种饼干;每袋丙类礼包有7包
种饼干;每袋丙类礼包有7包![]() 种饼干、1包
种饼干、1包![]() 种饼干、4包
种饼干、4包![]() 种饼干.已知甲每袋成本是该袋中
种饼干.已知甲每袋成本是该袋中![]() 种饼干成本的3倍,利润率为
种饼干成本的3倍,利润率为![]() ,每袋乙的成本是其售价的
,每袋乙的成本是其售价的![]() ,利润是每袋甲利润的
,利润是每袋甲利润的![]() ;每袋丙礼包利润率为
;每袋丙礼包利润率为![]() .若该网店12月12日当天销售甲、乙、丙三种礼包袋数之比为
.若该网店12月12日当天销售甲、乙、丙三种礼包袋数之比为![]() ,则当天该网店销售总利润率为__________.
,则当天该网店销售总利润率为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
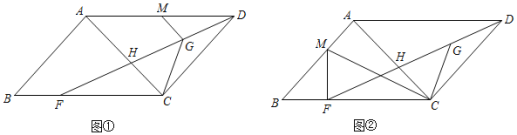
【题目】如图,ABCD中,DF平分∠ADC交AC于点H,G为DH的中点.
(1)如图①,若M为AD的中点,AB⊥AC,AC=9,CF=8,CG=2![]() ,求GM;
,求GM;
(2)如图②,M为线段AB上一点,连接MF,满足∠MCD=∠BCG,∠MFB=∠BAC.求证:MC=2CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )

A. 以相同速度行驶相同路程,甲车消耗汽油最多
B. 以10km/h的速度行驶时,消耗1升汽油,甲车最少行驶5千米
C. 以低于80km/h的速度行驶时,行驶相同路程,丙车消耗汽油最少
D. 以高于80km/h的速度行驶时,行驶相同路程,丙车比乙车省油
查看答案和解析>>
科目:初中数学 来源: 题型:
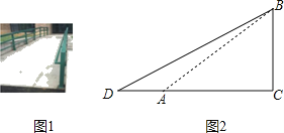
【题目】图1是无障碍通道,图2是其截面示意图,已知坡角∠BAC=30°,斜坡AB=4m,∠ACB=90°.现要对坡面进行改造,使改造后的坡角∠BDC=26.5°,需要把水平宽度AC增加多少m(结果精确到0.1)?(参考数据:![]() ≈1.73,sin26.5°≈0.45,cos26.5°≈0.90,tan26.5°≈0.50)
≈1.73,sin26.5°≈0.45,cos26.5°≈0.90,tan26.5°≈0.50)
查看答案和解析>>
科目:初中数学 来源: 题型:
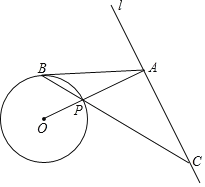
【题目】如图,已知直线l与⊙O无公共点,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长交直线l于点C,使得AB=AC.
(1)求证:AB是⊙O的切线;
(2)若BP=2![]() ,sin∠ACB
,sin∠ACB![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设美丽家园,某社区将辖区内的-块面积为1000m2的空地进行绿化,-部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用yl(元)与x(m2)的函数关系图象如图所示,栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.Olx2-20x+30000(0≤x≤1000).
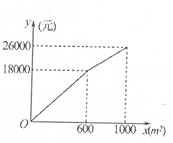
(1)求yl(元)与x(m2)的函数关系式;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与x的函数关系式,求绿化总费用W的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com