
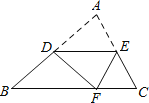
【题目】如图,在△ABC中,∠A=70°∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为______.
【答案】110°或50°.
【解析】
由内角和定理得出∠C=60°,根据翻折变换的性质知∠DFE=∠A=70°,再分∠EFC=90°和∠FEC=90°两种情况,先求出∠DFC度数,继而由∠BDF=∠DFC﹣∠B可得答案.
∵△ABC中,∠A=70°、∠B=50°,∴∠C=180°﹣∠A﹣∠B=60°,由翻折性质知∠DFE=∠A=70°,分两种情况讨论:
①当∠EFC=90°时,∠DFC=∠DFE+∠EFC=160°,则∠BDF=∠DFC﹣∠B=110°;
②当∠FEC=90°时,∠EFC=180°﹣∠FEC﹣∠C=30°,∴∠DFC=∠DFE+∠EFC=100°,∠BDF=∠DFC﹣∠B=50°;
综上:∠BDF的度数为110°或50°.
故答案为:110°或50°.


科目:初中数学 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC , 支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( ) (栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 . 车辆尺寸:长×宽×高)
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC , AD平分∠BAC , DE∥AC交AB于E , 则S△EBD:S△ABC=( ) 
A.1:2
B.1:4
C.1:3
D.2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形OABC的顶点A,B的坐标分别为A(6,0),B(6,4),D是BC的中点,动点P从O点出发,以每秒1个单位长度的速度,沿着O→A→B→D运动,设点P运动的时间为t秒(0<t<13).
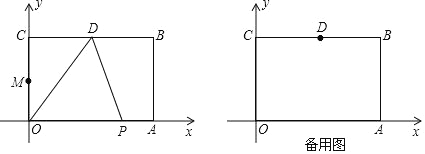
(1)①点D的坐标是(___,___);
②当点P在AB上运动时,点P的坐标是(___,___)(用t表示);
(2)写出△POD的面积S与t之间的函数关系式,并求出△POD的面积等于9时点P的坐标;
(3)当点P在OA上运动时,连接BP,将线段BP绕点P逆时针旋转,点B恰好落到OC的中点M处,则此时点P运动的时间t=___秒.(直接写出参考答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题,真命题是( ) 
A.如图,如果OP平分∠AOB,那么,PA=PB
B.三角形的一个外角大于它的一个内角
C.如果两条直线没有公共点,那么这两条直线互相平行
D.有一组邻边相等的矩形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
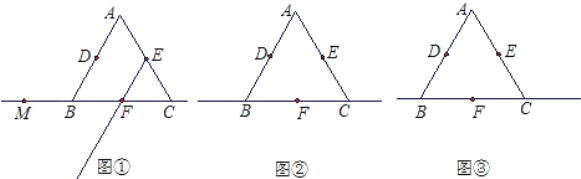
【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?画出图形,不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2﹣4x+3向上平移至顶点落在x轴上,如图所示,则两条抛物线、对称轴和y轴围成的图形的面积S(图中阴影部分)是( ) 
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论: ①b2>4ac;
②abc>0;
③2a﹣b=0;
④8a+c<0;
⑤9a+3b+c<0.
其中结论正确的是 . (填正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com