
【题目】现有多个全等直角三角形,先取三个拼成如图1所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,易得BP:QR:QR=3:1:2.
(1)若取四个直角三角形拼成如图2所示的形状,S为EF的中点,BS分别交AC,CD,DE于P,Q,R,则BP:PQ:QR:RS= ;
(2)若取五个直角三角形拼成如图3所示的形状,T为FG的中点,BT分别交AC,CD,DE,EF于P,Q,R,S,则BP:PQ:QR:RS:ST= .
【答案】4:1:3:2;5:1:4:2:3
【解析】解:(1)∵四个直角三角形是全等三角形,
∴AB=EF=CD,AB∥EF∥CD,BC=CE,AC∥DE,
∴BP:PR=BC:CE=1,
∵CD∥EF,
∴△BCQ∽△BES.
又∵BC=CE
∴CQ=![]() =
=![]() ,
,
∴DQ=![]()
∵AB∥CD,
∴∠ABP=∠DQR.
又∵∠BAP=∠QDR,
∴△BAP∽△QDR.
∴BP:QR=4:3.
∴BP:PQ:QR=4:1:3,
∵DQ∥SE,
∴QR:RS=DQ:SE=3:2,
∴BP:PQ:QR:RS=4:1:3:2.
故答案为:4:1:3:2;
(2)∵五个直角三角形是全等直角三角形
∴AB=CD=EF,AB∥CD∥EF,AC=DE=GF,AC∥DE∥GF,
BC=CE=EG,
∴BP=PR=RT,
∵AC∥DE∥GF,
∴△BPC∽△BER∽BTG,
∴PC=![]() =
=![]() ,RE=
,RE=![]() =
=![]() FG,
FG,
∴AP=![]() ,DR=
,DR=![]() ,FT=
,FT=![]()
∴AP:DR:FT=5:4:3.
∵AC∥DE∥GF,
∴∠BPA=∠QRD=∠STF.
又∵∠BAP=∠QDR=∠SFT,
∴△BAP∽△QDR∽△SFT.
∴BP:QR:ST=AP:DR:FT=5:4:3.
又∵BP:QR:RT=1:1:1,
∴BP:PQ:QR:RS:ST=5:(5﹣4):4:(5﹣3):3=5:1:4:2:3.
故答案为:5:1:4:2:3.
(1)首先证明△BCQ∽△BES,从而可求得CQ=![]() ,DQ=
,DQ=![]() EF,然后证明△BAP∽△QDR得到BP:QR=4:3从而可知:BP:PQ:QR=4:1:3,然后由DQ∥SE,可知:QR:RS=DQ:SE=3:2,从而可求得BP:PQ:QR:RS=4:1:3:2;
EF,然后证明△BAP∽△QDR得到BP:QR=4:3从而可知:BP:PQ:QR=4:1:3,然后由DQ∥SE,可知:QR:RS=DQ:SE=3:2,从而可求得BP:PQ:QR:RS=4:1:3:2;
(2) 由AC∥DE∥GF,可知:△BPC∽△BER∽BTG,能够求得:AP:DR:FT=5:4:3,然后再证明△BAP∽△QDR∽△SFT.,求得 BP:QR:ST=AP:DR:FT=5:4:3,因为∵BP:QR:RT=1:1:1,所以可求 得:BP:PQ:QR:RS:ST=5:1:4:2:3.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料: 小明遇到这样两个问题:
(1)如图1,AB是⊙O的直径,C是⊙O上一点,OD⊥AC,垂足为D,BC=﹣6,求OD的长; 
(2)如图2△ABC中,AB=6,AC=4,点D为BC的中点,求AD的取值范围. 对于问题(1),小明发现根据垂径定理,可以得出点D是AC的中点,利用三角形中位线定理可以解决;对于问题(2),小明发现延长AD到E,使DE=AD,连接BE,可以得到全等三角形,通过计算可以解决.
请回答:
问题(1)中OD长为;问题(2)中AD的取值范围是;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,∠BAC=90°,点D、E分别在AB、AC上,BE与CD相交于点F,AC=mEC,AB=2 ![]() EC,AD=nDB.
EC,AD=nDB. 
①当n=1时,如图4,在图中找出与CE相等的线段,并加以证明;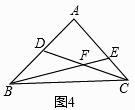
②直接写出 ![]() 的值(用含m、n的代数式表示).
的值(用含m、n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.8元,花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同,求粽子与咸鸭蛋的价格各多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+bx+![]() (a≠0)经过点A(﹣1,0)和B(3,0).
(a≠0)经过点A(﹣1,0)和B(3,0).
(1)求抛物线C1的解析式,并写出其顶点C的坐标;
(2)如图1,把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2 , 此时点A,C分别平移到点D,E处.设点F在抛物线C1上且在x轴的下方,若△DEF是以EF为底的等腰直角三角形,求点F的坐标;
(3)如图2,在(2)的条件下,设点M是线段BC上一动点,EN⊥EM交直线BF于点N,点P为线段MN的中点,当点M从点B向点C运动时:①tan∠ENM的值如何变化?请说明理由;②点M到达点C时,直接写出点P经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲经销商库存有1200套A品牌服装,每套进价400元,每套售价500元,一年内可卖完,现市场流行B品牌服装,每套进价300元,每套售价600元,但一年内只允许经销商一次性订购B品牌服装,一年内B品牌服装销售无积压,因甲经销商无流动资金可用,只有低价转让A品牌服装,用转让来的资金购进B品牌服装,并销售,经与乙经销商协商,甲、乙双方达成转让协议,转让价格y(元/套)与转让数量x(套)之间的函数关系式为y=﹣![]() x+360(100≤x≤1200),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
x+360(100≤x≤1200),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
(1)求转让后剩余的A品牌服装的销售款Q1(元)与x(套)之间的函数关系式;
(2)求B品牌服装的销售款Q2(元)与x(套)之间的函数关系式;
(3)求W(元)与x(套)之间的函数关系式,并求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将饰品售价调整为60+x(元/件)(x>0即售价上涨,x<0即售价下降),每月饰品销量为y(件),月利润为w(元).
(1)
直接写出y与x之间的函数关系式;
(2)如何确定销售价格才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元应如何控制销售价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】质地均匀的小正方体,六个面分别有数字“1”、“2”、“3”、“4”、“5”、“6”,同时投掷两枚,观察朝上一面的数字.
(1)求数字“1”出现的概率;
(2)求两个数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于点A、B,与直线AC:y=﹣x﹣6交y轴于点C,点D是抛物线的顶点,且横坐标为﹣2.
(1)求出抛物线的解析式.
(2)判断△ACD的形状,并说明理由.
(3)直线AD交y轴于点F,在线段AD上是否存在一点P,使∠ADC=∠PCF?若存在,直接写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com