
【题目】阅读下面材料: 小明遇到这样两个问题:
(1)如图1,AB是⊙O的直径,C是⊙O上一点,OD⊥AC,垂足为D,BC=﹣6,求OD的长; 
(2)如图2△ABC中,AB=6,AC=4,点D为BC的中点,求AD的取值范围. 对于问题(1),小明发现根据垂径定理,可以得出点D是AC的中点,利用三角形中位线定理可以解决;对于问题(2),小明发现延长AD到E,使DE=AD,连接BE,可以得到全等三角形,通过计算可以解决.
请回答:
问题(1)中OD长为;问题(2)中AD的取值范围是;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,∠BAC=90°,点D、E分别在AB、AC上,BE与CD相交于点F,AC=mEC,AB=2 ![]() EC,AD=nDB.
EC,AD=nDB. 
①当n=1时,如图4,在图中找出与CE相等的线段,并加以证明;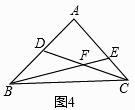
②直接写出 ![]() 的值(用含m、n的代数式表示).
的值(用含m、n的代数式表示).
【答案】
(1)解:如图1中,
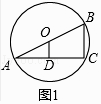
∵OD⊥AC,
∴AD=DC,
∵AO=OB,BC=6,
∴OD= ![]() BC=3.
BC=3.
(2)3;1<AD<5
(3)解:①结论:EF=CE.
理由:如图4中,延长CD到M使得DM=CD,连接BM.
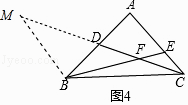
∵AD=DB,∠ADC=∠BDM,
∴△ADC≌△BDM,
∴BM=AC,∠M=∠ACD,
∴BM∥AC,
∴△CEF∽△MBF,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BF=mEF,
∴BE=(m+1)EF,
在Rt△BAE中,BE= ![]() =
= ![]() =(m+1)EC,
=(m+1)EC,
∴(m+1)EC=(m+1)EF,
∴EF=CE.
②结论: ![]() =
= ![]() .
.
理由:如图3中,作BM∥AC交CD的延长线于M.
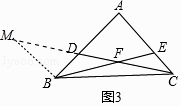
由△ADC∽△BDM,可得 ![]() =
= ![]() =n,
=n,
∴BM= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵AC=mEC,
∴BF= ![]() EF,
EF,
∴BE=(1+ ![]() )EF,
)EF,
在Rt△BAE中,BE= ![]() =
= ![]() =(m+1)EC,
=(m+1)EC,
∴(m+1)EC=(1+ ![]() )EF,
)EF,
∴ ![]() =
= ![]() .
.
【解析】(2)如图2中,延长AD到M,使得DM=AD,连接BM,CM. 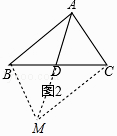
∵AD=DM,BD=CD,
∴四边形ABMC是平行四边形,
∴BM=AC=4,∵AB=6,
∴6﹣4<AM<6+4,
即2<2AD<10,
∴1<AD<5.


科目:初中数学 来源: 题型:
【题目】如图1,AB为⊙O的直径,点C,G都在⊙O上, ![]() =
= ![]() ,过点C作AB的垂线,垂足为D,连接BC,AC,BG,BG与AC相交于点E.
,过点C作AB的垂线,垂足为D,连接BC,AC,BG,BG与AC相交于点E. 
(1)求证:BG=2CD;
(2)若⊙O的直径为5 ![]() ,BC=5,求CE的长;
,BC=5,求CE的长;
(3)如图2,在(2)条件下,延长CD,ED,分别与⊙O相交于点M,N,连接MN,求MN的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知:矩形ABCD中,AC、BD是对角线,分别延长AD至E,延长CD至F,使得DE=AD,DF=CD. 
(1)求证:四边形ACEF为菱形.
(2)如图2,过E作EG⊥AC的延长线于G,若AG=8,cos∠ECG= ![]() ,则AD= (直接填空)、
,则AD= (直接填空)、
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )
A.![]()
B.6
C.![]()
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有多个全等直角三角形,先取三个拼成如图1所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,易得BP:QR:QR=3:1:2.
(1)若取四个直角三角形拼成如图2所示的形状,S为EF的中点,BS分别交AC,CD,DE于P,Q,R,则BP:PQ:QR:RS= ;
(2)若取五个直角三角形拼成如图3所示的形状,T为FG的中点,BT分别交AC,CD,DE,EF于P,Q,R,S,则BP:PQ:QR:RS:ST= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com