
【题目】如图1,AB为⊙O的直径,点C,G都在⊙O上, ![]() =
= ![]() ,过点C作AB的垂线,垂足为D,连接BC,AC,BG,BG与AC相交于点E.
,过点C作AB的垂线,垂足为D,连接BC,AC,BG,BG与AC相交于点E. 
(1)求证:BG=2CD;
(2)若⊙O的直径为5 ![]() ,BC=5,求CE的长;
,BC=5,求CE的长;
(3)如图2,在(2)条件下,延长CD,ED,分别与⊙O相交于点M,N,连接MN,求MN的长. 
【答案】
(1)证明:

如图,延长CD交⊙O于点F,
∵CD⊥AB,
∴ ![]() ,CF=2CD,
,CF=2CD,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴BG=CF,
∵CF=2CD
∴BG=2CD
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=5 ![]() ,BC=5,
,BC=5,
∴AC= ![]() =10,
=10,
∵ ![]() =
= ![]() ,
,
∴∠CBG=∠BAC,
∵∠BCE=∠ACB,
∴△BCE∽△ACB,
∴ ![]() ,
,
∴ ![]() ,
,
∴CE=2.5
(3)过点E作EI⊥AB于点I,过点N作NH⊥AB于点H,作NF⊥CM于点F,
连接ON,
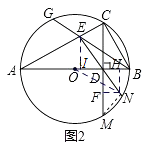
易证△BCD∽△CAB,
∴BC2=BDAB,
∴BD= ![]() ,
,
∴AD=5 ![]() ﹣
﹣ ![]() =4
=4 ![]() ,
,
由(2)可知:CE= ![]() ,
,
∴AE=10﹣ ![]() =
= ![]() ,
,
∵EI∥CD,
∴△AEI∽△ACD,
∴ ![]() ,
,
∴AI=3 ![]() ,
,
∴DI=AD﹣AI= ![]()
∵EI∥HN,
∴△EID∽△NHD,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
设NH=3x,DH=2x,
∵OD=OB﹣BD= ![]()
![]() ,
,
∴OH=OD+DH= ![]() +2x,
+2x,
在Rt△OHN中,
由勾股定理可得:( ![]()
![]() )2=(
)2=( ![]() +2x)2+(3x)2,
+2x)2+(3x)2,
∴13x2+6 ![]() x﹣20=0,
x﹣20=0,
x= ![]() ,
,
∵x>0,
∴x= ![]()
由勾股定理可知:CD=2 ![]() ,
,
∴DM=CD=2 ![]() ,
,
∴MF=2 ![]() ﹣3x,NF=DH=2x,
﹣3x,NF=DH=2x,
∴由勾股定理可求得:MN2=MF2+DH2,
∴MN2=20﹣12 ![]() x+13x2=40﹣18
x+13x2=40﹣18 ![]() x=
x= ![]() ,
,
∴MN= ![]()
【解析】(1)如图1,延长CD交⊙O于点F,由垂径定理可知,2CD=CF,所以只需要证明BG=CF即可;(2)由勾股定理可求得AC=10,再利用 ![]() ,可知∠CBG=∠BAC,所以可证明△BCE∽△ACB,然后利用对应边的比相等即可求出CE;(3)过点E作EI⊥AB于点I,过点N作NH⊥AB于点H,作NF⊥CM于点F,连接ON,利用相似三角形的性质和勾股定理分别求出BD、EI、ID的长度,并求出
,可知∠CBG=∠BAC,所以可证明△BCE∽△ACB,然后利用对应边的比相等即可求出CE;(3)过点E作EI⊥AB于点I,过点N作NH⊥AB于点H,作NF⊥CM于点F,连接ON,利用相似三角形的性质和勾股定理分别求出BD、EI、ID的长度,并求出 ![]() 的比值,利用勾股定理求出NH、DH的长度,进而求出MN的长度.
的比值,利用勾股定理求出NH、DH的长度,进而求出MN的长度.


科目:初中数学 来源: 题型:
【题目】已知直线y=﹣ ![]() x+3与两坐标轴分别相交于A,B两点,若点P,Q分别是线段AB,OB上的动点,且点P不与A,B重合,点Q不与O,B重合.
x+3与两坐标轴分别相交于A,B两点,若点P,Q分别是线段AB,OB上的动点,且点P不与A,B重合,点Q不与O,B重合.
(1)若OP⊥AB于点P,△OPQ为等腰三角形,这时满足条件的点Q有几个?请直接写出相应的OQ的长;
(2)当点P是AB的中点时,若△OPQ与△ABO相似,这时满足条件的点Q有几个?请分别求出相应的OQ的长;
(3)试探究是否存在以点P为直角顶点的Rt△OPQ?若存在,求出相应的OQ的范围,并求出OQ取最小值时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料

如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB,EF的中点均为O,连结BF,CD、CO,显然点C,F,O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB,EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出 ![]() 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),扇形AOB中,OA=10,∠AOB=36°.若固定B点,将此扇形依顺时针方向旋转,得一新扇形A′O′B,其中O′点在直线BA上,如图(2)所示,则O点旋转至O′点所经过的轨迹长度(弧长)为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究证明:
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为;
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的弦BC长为8,点A是⊙O上一动点,且∠BAC=45°,点D,E分别是BC,AB的中点,则DE长的最大值是( ) 
A.4
B.4 ![]()
C.8
D.8 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 小明遇到这样两个问题:
(1)如图1,AB是⊙O的直径,C是⊙O上一点,OD⊥AC,垂足为D,BC=﹣6,求OD的长; 
(2)如图2△ABC中,AB=6,AC=4,点D为BC的中点,求AD的取值范围. 对于问题(1),小明发现根据垂径定理,可以得出点D是AC的中点,利用三角形中位线定理可以解决;对于问题(2),小明发现延长AD到E,使DE=AD,连接BE,可以得到全等三角形,通过计算可以解决.
请回答:
问题(1)中OD长为;问题(2)中AD的取值范围是;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,∠BAC=90°,点D、E分别在AB、AC上,BE与CD相交于点F,AC=mEC,AB=2 ![]() EC,AD=nDB.
EC,AD=nDB. 
①当n=1时,如图4,在图中找出与CE相等的线段,并加以证明;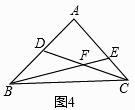
②直接写出 ![]() 的值(用含m、n的代数式表示).
的值(用含m、n的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com