
����Ŀ����ֱ֪��y=�� ![]() x+3����������ֱ��ཻ��A��B���㣬����P��Q�ֱ����߶�AB��OB�ϵĶ��㣬�ҵ�P����A��B�غϣ���Q����O��B�غϣ�
x+3����������ֱ��ཻ��A��B���㣬����P��Q�ֱ����߶�AB��OB�ϵĶ��㣬�ҵ�P����A��B�غϣ���Q����O��B�غϣ�
��1����OP��AB�ڵ�P����OPQΪ���������Σ���ʱ���������ĵ�Q�м�������ֱ��д����Ӧ��OQ�ij���
��2������P��AB���е�ʱ������OPQ���ABO���ƣ���ʱ���������ĵ�Q�м�������ֱ������Ӧ��OQ�ij���
��3����̽���Ƿ�����Ե�PΪֱ�Ƕ����Rt��OPQ�������ڣ������Ӧ��OQ�ķ�Χ�������OQȡ��Сֵʱ��P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��ͼ1�У����������ĵ�Q��������
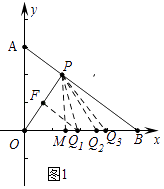
���ɣ���PM��OB��M����OP�Ĵ�ֱƽ���߽�OP��F����OB��Q1����Q1P=Q1O����OPQ1�ǵ��������Σ���ʱOQ1= ![]() OB=2��
OB=2��
��A��0��3����B��4��0����
��OA=3��OB=4��AB=5��
��OP��AB��
�� ![]() OAOB=
OAOB= ![]() ABOP��
ABOP��
��OP= ![]() =
= ![]() ��
��
��OQ2=OPʱ����OPQ2�ǵ��������Σ���ʱOQ2= ![]() ��
��
��PO=PQ3ʱ����PM��OQ3��
��OQ3=2OM��
�ߡ�POM=��POQ3����PMO=��OPB��
���OPM�ס�OBP��
��OP2=OMOB��
��OM= ![]() =
= ![]() ��
��
��OQ3= ![]() ��
��
������������OPQΪ����������ʱ�����������ĵ�Q��������OQ�ij�Ϊ2�� ![]() ��
�� ![]()
��2��
�⣺��ͼ2�У����������ĵ�Q��2����
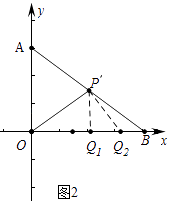
���ɣ���PQ1��OB��Q1��Q2P��OP��Q2��
��PA=PB����AOB=90�㣬
��PA=PB=PO��
���POQ1=��ABO���ߡ�PQ1O=��AOB��
���OPQ1�ס�BAO��
��PA=PB��PQ1��OA��
��OQ1=BQ1= ![]() OB=2��
OB=2��
�ߡ�POQ2=��ABO����OPQ2=��AOB��
���OPQ2�ס�BOA��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��OQ2= ![]() ��
��
������������OPQ���ABO����ʱ�����������ĵ�Q��2����OQ�ij�Ϊ2�� ![]()
��3��
�⣺���ڣ��������£�
��ͼ3�У���OQΪֱ������G������G��AB�����ڵ�Pʱ����OPQ=90�㣬��ʱOQ��ֵ��С��

����OG=GP=r��
��AO=AP=3��
��PB=AB=AP=2��
��Rt��PBG�У��ߡ�GPB=90�㣬PG=r��BG=4��r��PB=2��
��r2+22=��4��r��2��
��r= ![]() ��
��
��OQ=2r=3��
�൱3��OQ��4ʱ����OPQ��Ϊֱ�������Σ�
��PM��OB��M��
��PM��OA��
�� ![]() =
= ![]() =
= ![]() ��
��
�� ![]() =
= ![]() =
= ![]() ��
��
��PM= ![]() ��BM=
��BM= ![]() ��
��
��OM=4�� ![]() =
= ![]() ��
��
��OQȡ��Сֵʱ��P�����꣨ ![]() ��
�� ![]() ��
��
����������1����ͼ1�У����������ĵ�Q���������������������ۼ��ɢ�QO=QP����OP=OQ����PO=PQ����2����ͼ2�У����������ĵ�Q��2������PQ1��OB��Q1 �� Q2P��OP��Q2 �� ����֤��Q1��Q2�����������������������ε����ʼ��ɽ�����⣮��3�����ڣ���OQΪֱ������G������G��AB�����ڵ�Pʱ����OPQ=90�㣬��ʱOQ��ֵ��С���ɴ����OQ�����ɽ�����⣮
�����㾫����������Ĺؼ�����������������ε����ʵ����֪ʶ�����յ��������ε���������ȣ���ƣ��ȱ߶ԵȽǣ����Լ������������ε��ж������⣬�˽����������ε��ж�����:���Ƕ�Ӧ��ȣ������������ƣ�ASA����ֱ�������α�б���ϵĸ߷ֳɵ�����ֱ�������κ�ԭ���������ƣ� ���߶�Ӧ�ɱ����Ҽн���ȣ������������ƣ�SAS�������߶�Ӧ�ɱ����������������ƣ�SSS����


 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ס���������ֱ��������ABCD�Ķ���A��Cͬʱ�������εı߿�ʼ�ƶ�������˳ʱ�뷽���У��ҵ�����ʱ�뷽���У������ٶ����ҵ��ٶȵ�3���������ǵ�2015�������ڱ��ϣ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����P��a��b���͵�Q��a��b�䣩���������¶��壺��b��= ![]() ����Ƶ�QΪ��P���ޱ�㣮���磺�㣨2��3�����ޱ��������ǣ�2��3�����㣨��2��5�����ޱ��������ǣ���2����5����
����Ƶ�QΪ��P���ޱ�㣮���磺�㣨2��3�����ޱ��������ǣ�2��3�����㣨��2��5�����ޱ��������ǣ���2����5����
��1���㣨 ![]() ��1�����ޱ�����������
��1�����ޱ�����������
��2���жϵ�A����2����1����B����1��2���У���һ�����Ǻ���y= ![]() ͼ����ijһ������ޱ�㣿��˵�����ɣ�
ͼ����ijһ������ޱ�㣿��˵�����ɣ�
��3������P��a��b���ں���y=��x+3��ͼ���ϣ����ޱ��Q��a��b�䣩���������ȡֵ��Χ�ǩ�6��b��ܩ�3����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������˾Ϊ��������Ϊ����ᡱ�����60000Ԫ����֪�ҹ�˾�ȼ�˾�˾����40Ԫ����˾���������ҹ�˾��������20%��
�������������Ϣ�����һ���÷�ʽ���̽�������⣬��д�������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������5�·ݣ�ijУ���꼶ѧ���μ����������п��������ԣ�Ϊ���˽��У���꼶��1����ͬѧ���п������������ȫ��ѧ�����п������ɼ�������ͳ�ƣ����������²�������Ƶ���ֲ����������������ͳ��ͼ����ͼ��������ͼ���е���Ϣ����������⣺ 
��1����ȫ��ѧ��������m��ֵ��
��2��ֱ��ѧ���ð�ѧ�����п������ɼ�����λ�������ĸ������Σ�
��3���ð��п������ɼ����ֹ���3�ˣ���������2�ˣ�Ů��1�ˣ��������3�������ѡȡ2�˵����꼶���о��齻�������á��б���������״ͼ�������ǡ��ѡ��һ��һŮ�ĸ��ʣ�
���� | �����Σ��֣� | Ƶ�� |
A | 36��x��41 | 2 |
B | 41��x��46 | 5 |
C | 46��x��51 | 15 |
D | 51��x��56 | m |
E | 56��x��61 | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧС���ø�Ϊ1.2����������һ��ѧ¥�ĸ�CD����ͼ����CDһ�������A������������ý�ѧ¥����D������Ϊ�£�����A��C֮��ѡһ��B����B�������ѧ¥����D������Ϊ�������A��B֮��ľ���Ϊ4�ף���tan��=1.6��tan��=1.2���������������ѧ¥�ĸ��� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B��C������ֱ�Ϊ��1��0������0��1��������1��0����һ���綯��ߴ�����ԭ��0��������һ����Ծ����P1 �� ʹ�õ�P1���O���ڵ�A�����ĶԳƣ��ڶ�����Ծ����P2 �� ʹ�õ�P2���P1���ڵ�B�����ĶԳƣ���������Ծ����P3 �� ʹ�õ�P3���P2���ڵ�C�����ĶԳƣ����Ĵ���Ծ����P4 �� ʹ�õ�P4���P3���ڵ�A�����ĶԳƣ��������Ծ����P5 �� ʹ�õ�P5���P4���ڵ�B�����ĶԳƣ����մ˹����ظ���ȥ�����P7�������� �� ��P2016������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ABΪ��O��ֱ������C��G���ڡ�O�ϣ� ![]() =
= ![]() ������C��AB�Ĵ��ߣ�����ΪD������BC��AC��BG��BG��AC�ཻ�ڵ�E��
������C��AB�Ĵ��ߣ�����ΪD������BC��AC��BG��BG��AC�ཻ�ڵ�E�� 
��1����֤��BG=2CD��
��2������O��ֱ��Ϊ5 ![]() ��BC=5����CE�ij���
��BC=5����CE�ij���
��3����ͼ2���ڣ�2�������£��ӳ�CD��ED���ֱ����O�ཻ�ڵ�M��N������MN����MN�ij��� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���D��BC���е㣬��E��F�ֱ����߶�AD�����ӳ����ϣ���DE=DF������������������BE��EC����BF��CE����AB=AC������ѡ��һ������ʹ�ı���BECF�����Σ�����Ϊ�����������ֻ��д��ţ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com