练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，且DE=DF．给出下列条件：①BE⊥EC；②BF∥CE；③AB=AC；从中选择一个条件使四边形BECF是菱形，你认为这个条件是（只填写序号）．

    【答案】③
    【解析】解：选择条件③AB=AC时，四边形BECF是菱形；理由如下：
    ∵点D是BC的中点，
    ∴BD=CD，
    又∵DE=DF，
    ∴四边形BECF是平行四边形，
    ∵AB=AC，BD=CD，
    ∴AD⊥BC（三线合一），
    即EF⊥BC，
    ∴四边形BECF是菱形．
    故答案为③.
    根据题意易证得四边形BECF是平行四边形；添加①BE⊥EC时，只能说明它是矩形；添加②BF∥CE时，没有意义；添加③AB=AC时，根据对角线互相垂直的平行四边形是菱形证明.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知直线y=﹣ x+3与两坐标轴分别相交于A，B两点，若点P，Q分别是线段AB，OB上的动点，且点P不与A，B重合，点Q不与O，B重合．
    （1）若OP⊥AB于点P，△OPQ为等腰三角形，这时满足条件的点Q有几个？请直接写出相应的OQ的长；
    （2）当点P是AB的中点时，若△OPQ与△ABO相似，这时满足条件的点Q有几个？请分别求出相应的OQ的长；
    （3）试探究是否存在以点P为直角顶点的Rt△OPQ？若存在，求出相应的OQ的范围，并求出OQ取最小值时点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究证明：
    （1）如图1，在△ABC中，AB=AC，点E是BC上的一个动点，EG⊥AB，EF⊥AC，CD⊥AB，点G，F，D分别是垂足．求证：CD=EG+EF；
    猜想探究：

    （2）如图2，在△ABC中，AB=AC，点E是BC的延长线上的一个动点，EG⊥AB于G，EF⊥AC交AC延长线于F，CD⊥AB于D，直接猜想CD、EG、EF之间的关系为；

    （3）如图3，边长为10的正方形ABCD的对角线相交于点O、H在BD上，且BH=BC，连接CH，点E是CH上一点，EF⊥BD于点F，EG⊥BC于点G，则EF+EG= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的弦BC长为8，点A是⊙O上一动点，且∠BAC=45°，点D，E分别是BC，AB的中点，则DE长的最大值是（ ）

    A.4
    B.4
    C.8
    D.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2015年6月28日，“合福高铁”正式开通，对南平市的旅游产业带来了新的发展机遇．某旅行社抽样调查了2015年8月份该社接待来南平市若干个景点旅游的人数，并将调查结果绘制成如下两幅不完整的统计图表，请根据图表信息回答下列问题：

    景点

    频数
    （人数）

    频率

    九曲溪

    116

    0.29

    归宗岩

    0.25

    天成奇峡

    84

    0.21

    溪源峡谷

    64

    0.16

    华阳山

    36

    0.09


    （1）此次共调查人，
    （2）补全条形统计图；
    （3）由上表提供的数据可以制成扇形统计图，则“天成奇峡”所对扇形的圆心角为°；
    （4）该旅行社预计今年8月份将要接待来以上景点的游客约2 500人，根据以上信息，请你估计去“九曲溪”的游客大约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△A1A2A3 ， △A3A4A5 ， △A5A6A7 ， △A7A8A9 ， …，都是等边三角形，且点A1 ， A3 ， A5 ， A7 ， A9的坐标分别为A1（3，0），A3（1，0），A5（4，0），A7（0，0），A9（5，0），依据图形所反映的规律，则A100的坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在矩形ABCD中， =a，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．

    （1）如图1，当DH=DA时，填空：∠HGA=度；
    （2）如图1，当DH=DA时，若EF∥HG，求∠AHE的度数，并求此时的最小值；
    （3）如图3，∠AEH=60°，EG=2BG，连接FG，交边DC于点P，且FG⊥AB，G为垂足，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料： 小明遇到这样两个问题：

    （1）如图1，AB是⊙O的直径，C是⊙O上一点，OD⊥AC，垂足为D，BC=﹣6，求OD的长；
    （2）如图2△ABC中，AB=6，AC=4，点D为BC的中点，求AD的取值范围． 对于问题（1），小明发现根据垂径定理，可以得出点D是AC的中点，利用三角形中位线定理可以解决；对于问题（2），小明发现延长AD到E，使DE=AD，连接BE，可以得到全等三角形，通过计算可以解决．

    请回答：
    问题（1）中OD长为；问题（2）中AD的取值范围是；
    参考小明思考问题的方法，解决下面的问题：
    （3）如图3，△ABC中，∠BAC=90°，点D、E分别在AB、AC上，BE与CD相交于点F，AC=mEC，AB=2 EC，AD=nDB．
    ①当n=1时，如图4，在图中找出与CE相等的线段，并加以证明；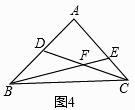

    ②直接写出 的值（用含m、n的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】端午节前夕，小东的父母准备购买若干个粽子和咸鸭蛋（每个粽子的价格相同，每个咸鸭蛋的价格相同）．已知粽子的价格比咸鸭蛋的价格贵1.8元，花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同，求粽子与咸鸭蛋的价格各多少？

    查看答案和解析>>

    同步练习册答案