
【题目】阅读材料

如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB,EF的中点均为O,连结BF,CD、CO,显然点C,F,O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB,EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出 ![]() 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)
【答案】
(1)
解:猜想:BF=CD.理由如下:
如答图②所示,连接OC、OD.

∵△ABC为等腰直角三角形,点O为斜边AB的中点,
∴OB=OC,∠BOC=90°.
∵△DEF为等腰直角三角形,点O为斜边EF的中点,
∴OF=OD,∠DOF=90°.
∵∠BOF=∠BOC+∠COF=90°+∠COF,∠COD=∠DOF+∠COF=90°+∠COF,
∴∠BOF=∠COD.
∵在△BOF与△COD中,

∴△BOF≌△COD(SAS),
∴BF=CD
(2)
解:答:(1)中的结论不成立.
如答图③所示,连接OC、OD.
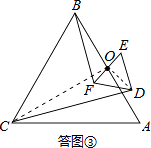
∵△ABC为等边三角形,点O为边AB的中点,
∴ ![]() =tan30°=
=tan30°= ![]() ,∠BOC=90°.
,∠BOC=90°.
∵△DEF为等边三角形,点O为边EF的中点,
∴ ![]() =tan30°=
=tan30°= ![]() ,∠DOF=90°.
,∠DOF=90°.
∴ ![]() =
= ![]() =
= ![]() .
.
∵∠BOF=∠BOC+∠COF=90°+∠COF,∠COD=∠DOF+∠COF=90°+∠COF,
∴∠BOF=∠COD.
在△BOF与△COD中,
∵ ![]() =
= ![]() =
= ![]() ,∠BOF=∠COD,
,∠BOF=∠COD,
∴△BOF∽△COD,
∴ ![]() =
= ![]()
(3)
解:如答图④所示,连接OC、OD.
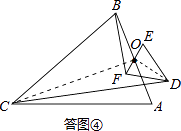
∵△ABC为等腰三角形,点O为底边AB的中点,
∴ ![]() =tan
=tan ![]() ,∠BOC=90°.
,∠BOC=90°.
∵△DEF为等腰三角形,点O为底边EF的中点,
∴ ![]() =tan
=tan ![]() ,∠DOF=90°.
,∠DOF=90°.
∴ ![]() =
= ![]() =tan
=tan ![]() .
.
∵∠BOF=∠BOC+∠COF=90°+∠COF,∠COD=∠DOF+∠COF=90°+∠COF,
∴∠BOF=∠COD.
在△BOF与△COD中,
∵ ![]() =
= ![]() =tan
=tan ![]() ,∠BOF=∠COD,
,∠BOF=∠COD,
∴△BOF∽△COD,
∴ ![]() =tan
=tan ![]()
【解析】(1)如答图②所示,连接OC、OD,证明△BOF≌△COD;(2)如答图③所示,连接OC、OD,证明△BOF∽△COD,相似比为 ![]() ;(3)如答图④所示,连接OC、OD,证明△BOF∽△COD,相似比为tan
;(3)如答图④所示,连接OC、OD,证明△BOF∽△COD,相似比为tan ![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC. 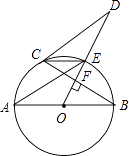
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司为“见义勇为基金会”各捐款60000元,已知乙公司比甲公司人均多捐40元,甲公司的人数比乙公司的人数多20%.
请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学小组用高为1.2米的仪器测量一教学楼的高CD,如图,距CD一定距离的A处,用仪器测得教学楼顶部D的仰角为β,再在A与C之间选一点B,由B处测出教学楼顶部D的仰角为α,测得A,B之间的距离为4米,若tanα=1.6,tanβ=1.2,则他们能求出教学楼的高吗? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1 . 使得点P1与点O关于点A成中心对称;第二次跳跃到点P2 , 使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3 , 使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4 , 使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5 , 使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P7的坐标是 , 点P2016的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点Bˊ处,DBˊ,EBˊ分别交边AC于点F,G,若∠ADF=80°,则∠EGC的度数为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为⊙O的直径,点C,G都在⊙O上, ![]() =
= ![]() ,过点C作AB的垂线,垂足为D,连接BC,AC,BG,BG与AC相交于点E.
,过点C作AB的垂线,垂足为D,连接BC,AC,BG,BG与AC相交于点E. 
(1)求证:BG=2CD;
(2)若⊙O的直径为5 ![]() ,BC=5,求CE的长;
,BC=5,求CE的长;
(3)如图2,在(2)条件下,延长CD,ED,分别与⊙O相交于点M,N,连接MN,求MN的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图. 根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com