
【题目】如图1,已知:矩形ABCD中,AC、BD是对角线,分别延长AD至E,延长CD至F,使得DE=AD,DF=CD. 
(1)求证:四边形ACEF为菱形.
(2)如图2,过E作EG⊥AC的延长线于G,若AG=8,cos∠ECG= ![]() ,则AD= (直接填空)、
,则AD= (直接填空)、
【答案】
(1)证明:∵DE=AD,DF=CD.
∴四边形ACEF是平行四边形,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴AE⊥CF,
∴四边形ACEF是菱形;
(2)2 ![]()
【解析】(2)解:∵四边形ACEF是菱形, ∴AC=CE,AD=ED,
∵EG⊥AC,cos∠ECG= ![]() =
= ![]() ,
,
∴CG= ![]() CE=
CE= ![]() AC,
AC,
∵AG=AC+CG=8,
∴CG=3,CE=AC=5,
∴EG= ![]() =4,
=4,
在Rt△AEG中,AE= ![]() =
= ![]() =4
=4 ![]() ,
,
∴AD= ![]() AE=2
AE=2 ![]() ;
;
故答案为:2 ![]() .
.
(1)先证明四边形ACEF是平行四边形,再由矩形的性质证出AE⊥CF,即可得出四边形ACEF是菱形;(2)由菱形的性质得出AC=CE,AD=ED,与三角函数得出CG= ![]() CE=
CE= ![]() AC,得出CG=3,CE=AC=5,由勾股定理求出EG=
AC,得出CG=3,CE=AC=5,由勾股定理求出EG= ![]() =4,在Rt△AEG中,由勾股定理求出AE=
=4,在Rt△AEG中,由勾股定理求出AE= ![]() =4
=4 ![]() ,即可得出AD的长.
,即可得出AD的长.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△A1A2A3 , △A3A4A5 , △A5A6A7 , △A7A8A9 , …,都是等边三角形,且点A1 , A3 , A5 , A7 , A9的坐标分别为A1(3,0),A3(1,0),A5(4,0),A7(0,0),A9(5,0),依据图形所反映的规律,则A100的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A在y轴上,点B的坐标为(1,2),将△AOB沿x轴向右平移得到△A′O′B′,点B的对应点B′恰好在函数y= ![]() (x>0)的图象上,此时点A移动的距离为 .
(x>0)的图象上,此时点A移动的距离为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 小明遇到这样两个问题:
(1)如图1,AB是⊙O的直径,C是⊙O上一点,OD⊥AC,垂足为D,BC=﹣6,求OD的长; 
(2)如图2△ABC中,AB=6,AC=4,点D为BC的中点,求AD的取值范围. 对于问题(1),小明发现根据垂径定理,可以得出点D是AC的中点,利用三角形中位线定理可以解决;对于问题(2),小明发现延长AD到E,使DE=AD,连接BE,可以得到全等三角形,通过计算可以解决.
请回答:
问题(1)中OD长为;问题(2)中AD的取值范围是;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,∠BAC=90°,点D、E分别在AB、AC上,BE与CD相交于点F,AC=mEC,AB=2 ![]() EC,AD=nDB.
EC,AD=nDB. 
①当n=1时,如图4,在图中找出与CE相等的线段,并加以证明;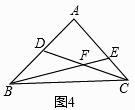
②直接写出 ![]() 的值(用含m、n的代数式表示).
的值(用含m、n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)、B(5,0)两点,与y轴交于C点,D为抛物线的顶点,E为抛物线上一点,且C、E关于抛物线的对称轴对称,分别作直线AE、DE.
(1)求此二次函数的关系式;
(2)在图1中,直线DE上有一点Q,使得△QCO≌△QBO,求点Q的坐标;
(3)如图2,直线DE与x轴交于点F,点M为线段AF上一个动点,有A向F运动,速度为每秒2个单位长度,运动到F处停止,点N由F处出发,沿射线FE方向运动,速度为每秒 ![]() 个单位长度,M、N两点同时出发,运动时间为t秒,当M停止时点N同时停止运动坐标平面内有一个动点P,t为何值时,以P、M、N、F为顶点的四边形是特殊的平行四边形.请直接写出t值.
个单位长度,M、N两点同时出发,运动时间为t秒,当M停止时点N同时停止运动坐标平面内有一个动点P,t为何值时,以P、M、N、F为顶点的四边形是特殊的平行四边形.请直接写出t值.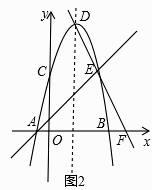
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC、BC及AB的延长线交于点D、E、F,且BF=BC,⊙O是△BEF的外接圆,连接BD. 
(1)求证:BD是⊙O的切线;
(2)求证:DEAC=BECE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PAPB=kAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将饰品售价调整为60+x(元/件)(x>0即售价上涨,x<0即售价下降),每月饰品销量为y(件),月利润为w(元).
(1)
直接写出y与x之间的函数关系式;
(2)如何确定销售价格才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元应如何控制销售价格?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com