
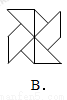
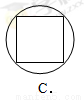
下列图形中,既是轴对称图形又是中心对称图形的是( ).
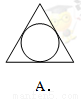

C.
【解析】
试题分析:本题考查了轴对称图形和中心对称图形的定义,A和D是轴对称图形,但不是中心对称图形,B是中心对称图形,但不是轴对称图形,只有C既是轴对称图形,又是中心对称图形.
故选:C.
考点:轴对称图形的定义;中心对称图形的定义.
考点分析: 考点1:图形的平移与旋转 定义:

科目:初中数学 来源:2014-2015学年安徽省八年级下学期开学考试数学试卷(解析版) 题型:解答题
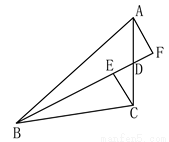
如图,已知BD为△ABC的中线,CE⊥BD于E,AF⊥BD于F.求证:BE+BF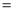 2BD
2BD
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:选择题
若关于 的一元二次方程的两个根为
的一元二次方程的两个根为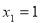 ,
,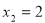 ,则这个方程是( )
,则这个方程是( )
A.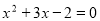 B.
B.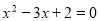
C.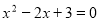 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:填空题
如图,有一圆弧形门拱的拱高AB为1m,跨度CD为4m,则这个圆弧形门拱的半径为 m.
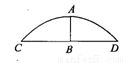
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:选择题
“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. B.
B.
C. D.
D.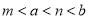
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题满分10分)某校学生参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如表所示:
销售单价x(单位:元/个) | 10 | 12 | 14 | 16 |
销售量y(单位:个) | 300 | 240 | 180 | 120 |
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;
(3)在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:填空题
如图,点A、B在反比例函数 的图像上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,△AOC的面积为6,则k的值为 .
的图像上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,△AOC的面积为6,则k的值为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题10分)我区某电子器件厂商投产一种新型电子产品,每件制造成本为18元,在试销过程中发现,每月销售量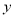 (万件)与销售单价
(万件)与销售单价 (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数 .(利润=售价﹣制造成本)
.(利润=售价﹣制造成本)
(1)写出每月的总利润 (万元)与销售单价
(万元)与销售单价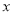 (元)之间的函数关系式;(3分)
(元)之间的函数关系式;(3分)
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?(4分)
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?(3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com