
(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线 上且CE=CA,试求∠DAE的度数;
上且CE=CA,试求∠DAE的度数;
(2)如果把第(1)题中“∠BAC=90°”的条件改为“∠BAC>90°”,其余条件不变,那么∠DAE与∠BAC有怎样的数量关系?

【考点】等腰三角形的性质;等腰直角三角形.
【分析】(1)由在△ABC中,∠BAC=90°,AB=AC,可求得∠ABC与∠ACB的度数,然后由BD=BA,CE=CA,分别求得∠BAD与∠CAE的度数,继而求得答案;
(2)首先设∠BAC=α,然后由AB=AC,用α表示出∠ABC与∠ACB的度数,继而由BD=BA,CE=CA,分别求得∠BAD与∠CAE的度数,则可求得答案.
【解答】解:(1)∠DAE=45°.
理由:∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
∴∠BAD= (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠CAE= ∠ACB=22.5°,
∠ACB=22.5°,
∴∠DAC=∠BAC﹣∠BAD=90°﹣67.5°=22.5°,
∴∠DAE=∠DAC+∠CAE=45°;
(2)∠DAE= ∠BAC.
∠BAC.
理由:设∠BAC=α,
∵AB=AC,
∴∠B=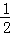 (180°﹣α),
(180°﹣α),
∵BA=BD,
∴∠BAD=∠BDA=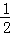 (180°﹣∠B),
(180°﹣∠B),
∴∠CAD=α﹣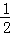 (180°﹣∠B)=α﹣90°+
(180°﹣∠B)=α﹣90°+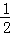 ∠B,
∠B,
∵CA=CE,
∴∠CAE=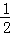 ∠ACB=
∠ACB=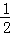 ∠B,
∠B,
∴∠DAE=α﹣90°+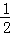 ∠B+
∠B+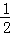 ∠B+
∠B+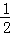 ∠B=α﹣90°+∠B,
∠B=α﹣90°+∠B,
∴∠DAE═α﹣90°+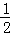 (180°﹣α)=
(180°﹣α)=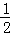 α,
α,
∴∠DAE=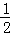 ∠BAC.
∠BAC.
【点评】此题考查了等腰三角形的性质以及三角形内角和定理.注意用设∠BAC=α,然后用α表示出各角是解此题的关键.


科目:初中数学 来源: 题型:
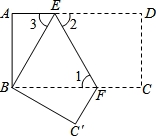
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)折叠后,DC的对应线段是__________,CF的对应线段是__________;
(2)若AB=8,DE=10,求CF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
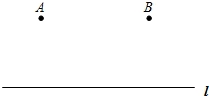
如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短.
(1)用尺规作图,作出点P; (作图要求:不写作法,保留作图痕迹)
(2)求出PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
点P(﹣2,﹣3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )
A.(﹣3,0) B.(﹣1,6) C.(﹣3,﹣6) D.(﹣1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去 B.带②去 C.带③去 D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在观测灯塔A北偏东60°方向上,则C处与灯塔A的距离是__________海里.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com