
如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短.
(1)用尺规作图,作出点P; (作图要求:不写作法,保留作图痕迹)
(2)求出PA+PB的最小值.
【考点】轴对称-最短路线问题;作图—应用与设计作图.
【分析】(1)首先作出A点的对称点A′,然后连接BA′,找到交点P点;
(2)首先连接AB,由题意知AB=3km,A A′=4km,然后由勾股定理求得A′B的长,即PA+PB的最小值.
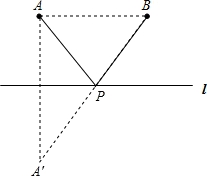
【解答】解:(1)作图,如右图,
作出A点的对称点A′,
连接BA′,找到交点P点;
(2)连接AB,由题意知AB=3km,A A′=4km,
在Rt△A A′B中,根据勾股定理得:A′B2=42+32,
∴A′B=5km,
即PA+PB=A′B=5km,
答:PA+PB的最小值是5km.
【点评】此题考查了最短路径问题以及勾股定理.注意准确找到点P是解此题的关键.


科目:初中数学 来源: 题型:
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下五个结论:
(1)AE=CF;(2)∠APE=∠CPF;(3)三角形EPF是等腰直角三角形;(4)S四边形AEPF= S△ABC;(5)EF=AP,
S△ABC;(5)EF=AP,
其中正确的有__________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,Rt△ABC中,∠B=90°,AB=9,BC=6,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段AN的长等于( )
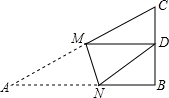
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线 上且CE=CA,试求∠DAE的度数;
上且CE=CA,试求∠DAE的度数;
(2)如果把第(1)题中“∠BAC=90°”的条件改为“∠BAC>90°”,其余条件不变,那么∠DAE与∠BAC有怎样的数量关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一次函数y=(m﹣5)x+6﹣2m的图象分别与x轴、y轴的相交于A、B两点,则m的取值范围是
( )

A.m<5 B.m<3 C.3<m<5 D.m>3
查看答案和解析>>
科目:初中数学 来源: 题型:
为绿化校园,某校计划购进A、B两种树苗,共21课.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.
(1)y与x的函数关系式为:__________;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com