
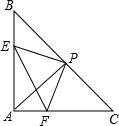
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下五个结论:
(1)AE=CF;(2)∠APE=∠CPF;(3)三角形EPF是等腰直角三角形;(4)S四边形AEPF= S△ABC;(5)EF=AP,
S△ABC;(5)EF=AP,
其中正确的有__________个.

4【考点】全等三角形的判定与性质;等腰直角三角形.
【分析】(1)通过证明△AEP≌△CFP就可以得出AE=CF,
(2)由∠EPA+∠FPA=90°,∠CPF+∠FPA=90°,就可以得出结论;
(3)由△AEP≌△CFP就可以PE=PF,即可得出结论;
(4)由S四边形AEPF=S△APE+S△APF.就可以得出S四边形AEPF=S△CPF+S△APF,就可以得出结论,
(5)由条件知AP=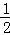 BC,当EF是△ABC的中位线时才有EF=AP,其他情况EF≠AP.
BC,当EF是△ABC的中位线时才有EF=AP,其他情况EF≠AP.
【解答】解:(1)∵∠EPA+∠FPA=∠EPF=90°,∠CPF+∠FPA=90°,
∴∠APE=∠CPF.故(1)正确.
∵AB=AC,∠BAC=90° ,
,
∴∠B=∠C=45°.
∵P是BC的中点,
∴BP=CP=AP=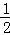 BC.∠BAP=∠CAP=45°.
BC.∠BAP=∠CAP=45°.
∴.∠BAP=∠C.
在△AEP和△CFP中
 ,
,
∴△AEP≌△CFP(ASA),
∴AE=CF,PE=PF,S△AEP=S△CFP,故(2)正确.
∴△EPF是等腰直角三角形.故(3)正确.
∵S四边形AEPF=S△APE+S△APF.
∴S四边形AEPF=S△CPF+S△APF=S△APC=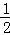 S△ABC.故(4)正确.
S△ABC.故(4)正确.
∵△ABC是等腰直角 三角形,P是BC的中点,
三角形,P是BC的中点,
∴AP=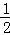 BC,
BC,
∵EF不是△ABC的中位线,
∴EF≠AP ,故(5)错误;
,故(5)错误;
∴正确的共有4个.
故答案为4.
【点评】本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,中位线的性质的运用,等腰直角三角形的判定定理的运用,三角形面积公式的运用,解答时灵活运用等腰直角三角形的性质求解是关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
在Rt△ABC中,∠ACB=90°,AC=24cm,AB=26cm,则其直角边BC的长为( )
A.6cm B.100cm C.15cm D.10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
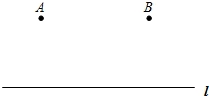
如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短.
(1)用尺规作图,作出点P; (作图要求:不写作法,保留作图痕迹)
(2)求出PA+PB的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com