
如图在△ABD和△ACE都是等边三角形,则△ADC≌△ABE的根据是( )
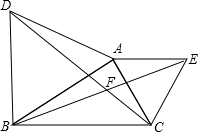
A.SSS B.SAS C.ASA D.AAS
B【考点】全等三角形的判定.
【分析】因为△ABD和△ACE都是等边三角形,所以有AD=AB,AC=AE,又因为∠DAB+∠BAC=∠EAC+∠BAC,所以∠DAC=∠BAE,故可根据SAS判定△ADC≌△ABE.
【解答】解:∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,
又∵∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
∴△ADC≌△ABE(SAS).
故选B.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下五个结论:
(1)AE=CF;(2)∠APE=∠CPF;(3)三角形EPF是等腰直角三角形;(4)S四边形AEPF= S△ABC;(5)EF=AP,
S△ABC;(5)EF=AP,
其中正确的有__________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一次函数y=(m﹣5)x+6﹣2m的图象分别与x轴、y轴的相交于A、B两点,则m的取值范围是
( )

A.m<5 B.m<3 C.3<m<5 D.m>3
查看答案和解析>>
科目:初中数学 来源: 题型:
为绿化校园,某校计划购进A、B两种树苗,共21课.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.
(1)y与x的函数关系式为:__________;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知,△ABC 是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
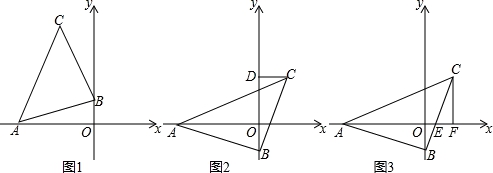
(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,﹣1),求点C的坐标;
(2)如图2,过点C作CD⊥y轴于D,请直接写出线段OA、OD、CD之间等量关系;
(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于F,问CF与AE有怎样的数量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com