
为绿化校园,某校计划购进A、B两种树苗,共21课.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.
(1)y与x的函数关系式为:__________;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
【考点】一次函数的应用.
【分析】(1)根据购买两种树苗所需费用=A种树苗费用+B种树苗费用,即可解答;
(2)根据购买B种树苗的数量少于A种树苗的数量,列出不等式,确定x的取值范围,再根据(1)得出的y与x之间的函数关系式,利用一次函数的增减性结合自变量的取值即可得出更合算的方案.
【解答】解:(1)y=90(21﹣x)+70x=﹣20x+1890,
故答案为:y=﹣20x+1890.
(2)∵购买B种树苗的数量少于A种树苗的数量,
∴x<21﹣x,
解得:x<10.5,
又∵x≥1,
∴x的取值范围为:1≤x≤10,且x为整数,
∵y=﹣20x+1890,k=﹣20<0,
∴y随x的增大而减小,
∴当x=10时,y有最小值,最小值为:﹣20×10+1890=1690,
∴使费用最省的方案是购买B种树苗10棵,A种树苗11棵,所需费用为1690元.
【点评】题考查的是一元一次不等式及一次函数的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系.


科目:初中数学 来源: 题型:
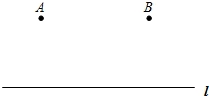
如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短.
(1)用尺规作图,作出点P; (作图要求:不写作法,保留作图痕迹)
(2)求出PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC的三个顶点和它内部的点P1,把△ABC分成3个互不重叠的小三角形;△ABC的三个顶点和它内部的点P1、P2,把△ABC分成5个互不重叠的小三角形;△ABC的三个顶点和它内部的点 P1、P2、P3,把△ABC分成7个互不重叠的小三角形;…△ABC的三个顶点和它内部的点 P1、P2、P3、…、Pn,把△ABC分成__________个互不重叠的小三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去 B.带②去 C.带③去 D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是__________(填序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com