练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    等边△ABC的两条角平分线BD与CE交于点O，则∠BOC等于__________．


    120°．

    【考点】等边三角形的性质．

    【分析】由已知条件根据等边三角形的性质、角平分线的性质求解．

    【解答】解：如图，

    ∵等边三角形ABC中，BD，CE分别是∠ABC，∠ACB的角的平分线，交于点O，

    ∴∠DBC=∠ECB=∠ACB=30°，

    ∴∠BOC=180°﹣（∠DBC+∠ECB）=120°．

    故答案为：120°．

    【点评】本题考查了等边三角形的性质，角的平分线的定义，三角形内角和定理，熟练掌握等边三角形的性质是解题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


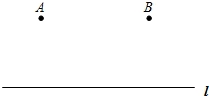
    如图：A村和B村在公路l同侧，且AB=3千米，两村距离公路都是2千米．现决定在公路l上建立一个供水站P，要求使PA+PB最短．

    （1）用尺规作图，作出点P； （作图要求：不写作法，保留作图痕迹）

    （2）求出PA+PB的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图在△ABD和△ACE都是等边三角形，则△ADC≌△ABE的根据是(     )

    A．SSS  B．SAS  C．ASA  D．AAS

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列长度（单位：cm）的三根小木棒，把它们首尾顺次相接能摆成一个三角形的是(     )

    A．1，2，3   B．5，6，7   C．6，8，18 D．3，3，6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知一个等腰三角形两内角的度数之比为1：2，则这个等腰三角形顶角的度数为(     )

    A．36°   B．36°或90° C．90°   D．60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行，在B处观测灯塔A位于南偏东75°方向上，轮船航行半小时到达C处，在观测灯塔A北偏东60°方向上，则C处与灯塔A的距离是__________海里．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，四边形ABCD中，∠B=90°，AB∥CD，M为BC边上的一点，且AM平分∠BAD，DM平分∠ADC．求证：

    （1）AM⊥DM；

    （2）M为BC的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AD是角平分线，E是AB上一点，AE=AC，EF∥BC交AC于F．下列结论①△ADC≌△ADE；②CE平分∠DEF；③AD垂直平分CE．其中正确的是__________（填序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是(     )

    A．      B．      C．     D．

    查看答案和解析>>

    同步练习册答案