
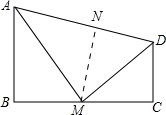
如图,四边形ABCD 中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:
中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:
(1)AM⊥DM;
(2)M为BC的中点.

【考点】角平分线的性质.
【专题】证明题.
【分析】(1)根据平行线的性质得到∠BAD+∠ADC=180°,根据角平分线的定义得到∠MAD+∠ADM=90°,根据垂直的定义得到答案;
(2)作NM⊥AD,根据角平分线的性质得到BM=MN,MN=CM,等量代换得到答案.
【解答】解:(1)∵AB∥CD,
∴∠BAD+∠ADC=180°,
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180°,
∴∠MAD+∠ADM=90°,
∴∠AMD=90°,
即AM⊥DM;
(2)作NM⊥AD交AD于N,
∵∠B=90°,AB∥CD,
∴BM⊥AB,CM⊥CD,
∵AM平分∠BAD,DM平分∠ADC,
∴BM=MN,MN=CM,
∴BM=CM,
即M为BC的中点.
【点评】本题考查的是角平分线的性质,掌握平行线的性质和角的平分线上的点到角的两边的距离相等是解题的关键.


科目:初中数学 来源: 题型:
如图,一次函数y=(m﹣5)x+6﹣2m的图象分别与x轴、y轴的相交于A、B两点,则m的取值范围是
( )

A.m<5 B.m<3 C.3<m<5 D.m>3
查看答案和解析>>
科目:初中数学 来源: 题型:
根据下列已知条件,能唯一画出△ABC的是( )
A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°
C.∠A=60°,∠B=45°,AB=4 D.∠C=90°,AB=6
查看答案和解析>>
科目:初中数学 来源: 题型:
已知,△ABC 是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
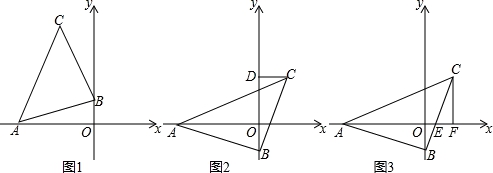
(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,﹣1),求点C的坐标;
(2)如图2,过点C作CD⊥y轴于D,请直接写出线段OA、OD、CD之间等量关系;
(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于F,问CF与AE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )
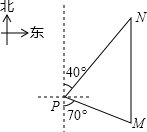
A.40海里 B.60海里 C.70海里 D.80海里
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com