
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘法运算,再计算加减运算即可得到结果;
(3)原式利用除法法则变形,再利用乘法分配律计算即可得到结果;
(4)将被除数与除数调换求出值,即可确定出原式的值.
解答 解:(1)原式=-8+9+0.25-$\frac{1}{4}$=1;
(2)原式=-30+$\frac{1}{25}$=-29$\frac{24}{25}$;
(3)原式=($\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$-$\frac{4}{5}$+$\frac{1}{6}$)×(-60)=-30-20-15+48-10=-27;
(4)($\frac{3}{5}$-$\frac{1}{6}$-$\frac{2}{3}$)÷(-$\frac{7}{30}$)=$\frac{18-5-20}{30}$÷(-$\frac{7}{30}$)=-$\frac{7}{30}$÷(-$\frac{7}{30}$)=1,
则原式=1.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
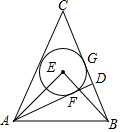 如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.
如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.7724×104元 | B. | 7.724×103元 | C. | 7.724×1011元 | D. | 0.7724×1012元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
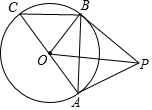 如图,已知AC是⊙O的直径,BC是⊙O的弦,P是⊙O外一点,连接PB,AB,OB,且∠PBA=∠ACB.
如图,已知AC是⊙O的直径,BC是⊙O的弦,P是⊙O外一点,连接PB,AB,OB,且∠PBA=∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
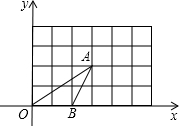 如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com