
【题目】如图,一副三角板的两个直角顶点重合在一起.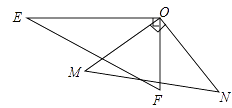
(1)若∠EON=140°,求∠MOF的度数;
(2)比较∠EOM与∠FON的大小,并写出理由;
(3)求∠EON+∠MOF的度数.
【答案】
(1)解:∵∠EOF=90°,∠EON=140°,
∴∠FON=50°,
∵∠MON=90°,
∴∠MOF=40°,
(2)解:∠EOM=∠FON,
∵∠EOM+∠MOF=∠FON+∠MOF=90°,
∴∠EOM=∠FON,
(3)解:∵∠EON+∠MOF=∠EOM+∠MOF+∠FON+∠MOF,
∴∠EON+∠MOF=∠EOF+∠MON=180°.
【解析】(1)由∠EOF=90°,∠EON=140°,即可求出∠FON=50°,然后由∠MON=90°,即可求出结果,
(2)由余角的性质即可推出∠EOM=∠FON,
(3)由图形可知∠EON+∠MOF=∠EOM+∠MOF+∠FON+∠MOF,即可推出∠EON+∠MOF的度数.


科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
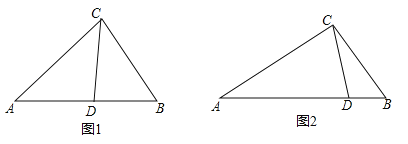
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平整的地面上,有若干个完全相同的棱长的小正方体堆成一个几何体(如图所示).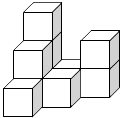
(1)这个几何体由个小正方体组成,请画出这个几何体的三视图;
(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有个正方体只有两个面是黄色,有个正方体只有三个面是黄色(注:该几何体与地面重合的部分不喷漆).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某酒店有三人间、双人间客房若干,各种房型每天的收费标准如下:
普通(元/间) | 豪华(元/间) | |
三人间 | 160 | 400 |
双人间 | 140 | 300 |
一个50人的旅游团到该酒店入住,选择了一些三人普通间和双人豪华间入住,且恰好住满.已知该旅游团当日住宿费用共计4020元,问该旅游团入住的三人普通间和双人豪华间各为几间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌手机的进价为1200元,按原价的八折出售可获利14%,则该手机的原售价为( )
A.1800元
B.1700元
C.1710元
D.1750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读句画图并回答问题: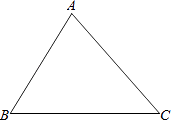
(1)过点A画AD⊥BC,垂足为D.比较AD与AB的大小:ADAB;
(2)用直尺和圆规作∠CDE,使∠CDE=∠ABC,且与AC交于点E.此时DE与AB的位置关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.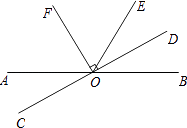
(1)若∠AOE=120°,求∠BOD的度数;
(2)写出图中所有与∠AOD互补的角: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何知识可以解决生活中许多距离最短的问题.让我们从书本一道习题入手进行知识探索.
(1)【回忆】
如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并说明理由.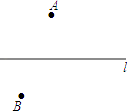
(2)【探索】
如图,A、B两个村庄在一条笔直的马路的两端,村庄 C在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置,并说明理由.
(3)如图,A、B、C、D四个村庄,现建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O的位置,并说明理由.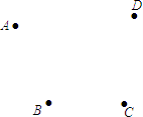
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com