
【题目】如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,求线段DE的长. 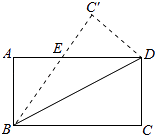
【答案】解:设ED=x,则AE=6﹣x, ∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠DBC;
由题意得:∠EBD=∠DBC,
∴∠EDB=∠EBD,
∴EB=ED=x;
由勾股定理得:
BE2=AB2+AE2 ,
即x2=9+(6﹣x)2 ,
解得:x=3.75,
∴ED=3.75
【解析】根据题意得到BE=DE,然后根据勾股定理得到关于线段AB、AE、BE的方程,解方程即可.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等),还要掌握翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,△ACB和△DCE均为等腰三角形,点A、D、E在同一直线上,连接BF.若∠CAB=∠CBA=∠CDE=∠CED=50°.
(1)求证:AD=BE;
(2)求∠AEB的度数.
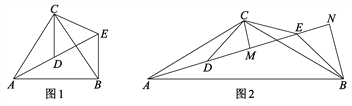
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.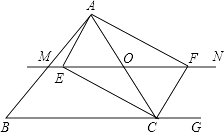
(1)试说明EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究
(1)探究发现 数学活动课上,小明说“若直线y=2x﹣1向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”
经过一番讨论,小组成员展示了他们的解答过程:
在直线y=2x﹣1上任取点A(0,﹣1),
向左平移3个单位得到点A′(﹣3,﹣1)
设向左平移3个单位后所得直线所对应的函数表达式为y=2x+n.
因为y=2x+n过点A′(﹣3,﹣1),
所以﹣6+n=﹣1,
所以n=5,
填空:所以平移后所得直线所对应函数表达式为
(2)类比运用 已知直线y=2x﹣1,求它关于x轴对称的直线所对应的函数表达式;
(3)拓展运用 将直线y=2x﹣1绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.点P(3,2)到x轴距离是3
B.在平面直角坐标系中,点(2,﹣3)和点(﹣2,3)表示同一个点
C.若y=0,则点M(x,y)在y轴上
D.在平面直角坐标系中,第三象限内点的横坐标与纵坐标同号
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】掷一枚正方体的骰子,各个面上分别标有数字1, 2,3,4,5,6,求下列事件发生的频率的大小:
①朝上的数字是奇数;
②朝上的数字能被3除余1;
③朝上的数字不是3的倍数;
④朝上的数字小于6;
⑤朝上的数字不小于3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com