
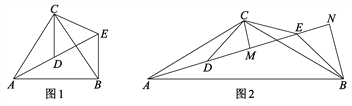
【题目】如图,△ACB和△DCE均为等腰三角形,点A、D、E在同一直线上,连接BF.若∠CAB=∠CBA=∠CDE=∠CED=50°.
(1)求证:AD=BE;
(2)求∠AEB的度数.
【答案】(1)见解析;(2)80°.
【解析】试题分析:(1)通过角的计算找出∠ACD=∠BCE,再结合△ACB和△DCE均为等腰三角形可得出“AC=BC,DC=EC”,利用全等三角形的判定(SAS)即可证出△ACD≌△BCE,由此即可得出结论AD=BE;
(2)结合(1)中的△ACD≌△BCE可得出∠ADC=∠BEC,再通过角的计算即可算出∠AEB的度数.
试题解析:(1)∵∠CAB=∠CBA=∠CDE=∠CED=50°,
∴∠ACB=∠DCE=180°-2×50°=80°,
∵∠ACB=∠ACD+∠DCB,∠DCE=∠DCB+∠BCE,
∴∠ACD=∠BCE,
∵△ACB和△DCE均为等腰三角形,
∴AC=BC,DC=EC,
在△ACD和△BCE中,有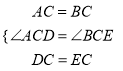 ,∴△ACD≌△BCE(SAS),∴AD=BE;
,∴△ACD≌△BCE(SAS),∴AD=BE;
(2)∵△ACD≌△BCE,∴∠ADC=∠BEC,
∵点A、D、E在同一直线上,且∠CDE=50°,
∴∠ADC=180°-∠CDE=130°,∴∠BEC=130°,
∵∠BEC=∠CED+∠AEB,且∠CED=50°,
∴∠AEB=∠BEC-∠CED=130°-50°=80°.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.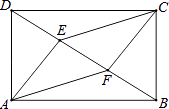
(1)求证:四边形AFCE是平行四边形;
(2)若AE⊥BD,AF=2 ![]() ,AB=4,求BF的长度.
,AB=4,求BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
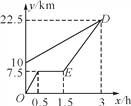
【题目】(本题满分7分)小亮、小明两人星期天8:00同时分别从A,B两地出发,沿同一条路线前往新华书店C.小明从B地步行出发,小亮骑自行车从A地出发途经B地,途中自行车发生故障,维修耽误了1 h,结果他俩11:00同时到达书店C.下图是他们距离A地的路程y(km)与所用时间x(h)之间的函数关系图象.请根据图中提供的信息,解答下列问题:
(1)求图中直线DE的函数解析式;
(2)若小亮的自行车不发生故障,且保持出发时的速度前行,则他出发多久可追上小明?此时他距离A地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A关于x轴对称点的坐标为(2,-1),则点A的坐标为:( )
A. (-2,1) B. (2,1) C. (-2,-1) D. (-1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外其他都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球是等可能的.你同意他的说法吗?为什么?
(2)搅匀后从中摸出一个球,请求出不是白球的概率;
(3)搅匀后从中任意摸出一个球,要使摸出红球的概率为![]() ,应添加几个红球?
,应添加几个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件能保证△ABC≌△ADC的是:①AB=AD,BC=DC;②∠1=∠3,∠4=∠2;③∠1=∠2,∠4=∠3;④∠1=∠2,AB=AD;⑤∠1=∠2,BC=DC.( )
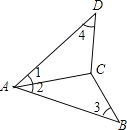
A. ①②③④⑤ B. ①②③④ C. ①③④ D. ①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com