
【题目】在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.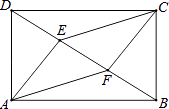
(1)求证:四边形AFCE是平行四边形;
(2)若AE⊥BD,AF=2 ![]() ,AB=4,求BF的长度.
,AB=4,求BF的长度.
【答案】
(1)
证明:连接AC,交BD于O,如图所示:
∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OC,OB=OD,
∵DE=FB,
∴OE=OF,
∴四边形AFCE是平行四边形
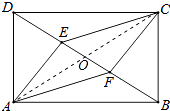
(2)
解:∵DE=EF=BF,AE⊥BD,
∴AD=AF=2 ![]() ,
,
∴BD= ![]() =
= ![]() =2
=2 ![]() ,
,
∴BF= ![]() BD=
BD= ![]()
【解析】(1)连接AC,由矩形的性质得出OA=OC,OB=OD,再由DE=FB,证出OE=OF,即可得出结论;(2)由线段垂直平分线的性质得出AD=AF,再根据勾股定理求出BD,即可得出BF.
【考点精析】解答此题的关键在于理解平行四边形的判定与性质的相关知识,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线________.
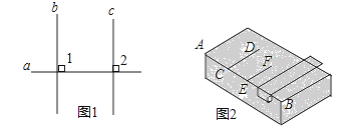
(1)它的理由如下:(如图1)
∵b⊥a,c⊥a,∴∠1=∠2=90°,
∴b∥c________
(2)如图2是木工师傅使用角尺画平行线,有什么道理?________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
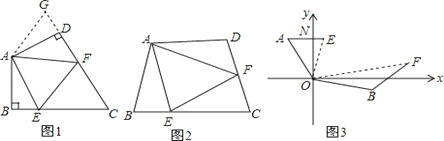
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD上述结论是否仍然成立,并说明理由;
∠BAD上述结论是否仍然成立,并说明理由;
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图形填空:
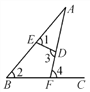
(1)若直线ED,BC被直线AB所截,则∠1和__________是同位角.
(2)若直线ED,BC被直线AF所截,则∠3和__________是内错角.
(3)∠1和∠3是直线AB,AF被直线__________所截构成的__________角.
(4)∠2和∠4是直线__________,__________被直线BC所截构成的__________角.
查看答案和解析>>
科目:初中数学 来源: 题型:
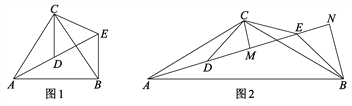
【题目】如图,△ACB和△DCE均为等腰三角形,点A、D、E在同一直线上,连接BF.若∠CAB=∠CBA=∠CDE=∠CED=50°.
(1)求证:AD=BE;
(2)求∠AEB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com