
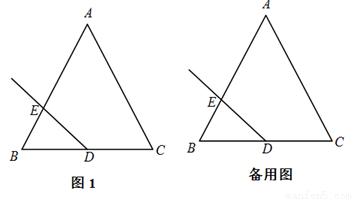
在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.
(1)依题意将图1补全;
(2)小华通过观察、实验提出猜想:在点E运动的过程中,始终有DE=DF.小华把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;
想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;
想法3:由等腰三角形三线合一,可得AD是∠BAC的角平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF…….
请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);
(3)在点E运动的过程中,直接写出BE,CF,AB之间的数量关系.
科目:初中数学 来源:2017届辽宁省盘锦市九年级下学期第二次模拟考试数学试卷(解析版) 题型:解答题
(本题满分10分)如图所示,一幢楼房AB背后有一台阶CD,台阶每层高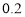 米,且AC=
米,且AC=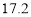 米,设太阳光线与水平地面的夹角为
米,设太阳光线与水平地面的夹角为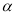 .当
.当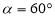 时,测得楼房在地面上的影长AE=
时,测得楼房在地面上的影长AE=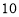 米,现有一只小猫睡在台阶的MN这层上晒太阳.(
米,现有一只小猫睡在台阶的MN这层上晒太阳.(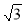 取
取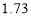 )
)
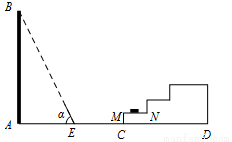
(1)求楼房的高度约为多少米?
(2)过了一会儿,当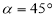 时,问小猫能否还晒到太阳?请说明理由.
时,问小猫能否还晒到太阳?请说明理由.
查看答案和解析>>
科目:初中数学 来源:广东省深圳市宝安区2016-2017学年七年级下学期期中考试数学试卷(解析版) 题型:选择题
已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B. 6 C.11 D.16
查看答案和解析>>
科目:初中数学 来源:2017届湖北省武汉市中考模拟数学试卷(一)(解析版) 题型:单选题
不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )
A. 摸出的3个白球 B. 摸出的是3个黑球
C. 摸出的是2个白球、1个黑球 D. 摸出的是2个黑球、1个白球
查看答案和解析>>
科目:初中数学 来源:2017届北京市平谷区4月初三统一练习(一)数学试卷(解析版) 题型:解答题
如图,在△ABC中,BD平分∠ABC交AC于D,EF垂直平分BD,分别交AB,BC,BD于E,F,G,连接DE,DF.
(1)求证:DE=DF;
(2)若∠ABC=30°,∠C=45°,DE=4,求CF的长.
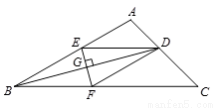
查看答案和解析>>
科目:初中数学 来源:2017届北京市平谷区4月初三统一练习(一)数学试卷(解析版) 题型:填空题
小米是一个爱动脑筋的孩子,他用如下方法作∠AOB的角平分线:作法:如图,
(1)在射线OA上任取一点C,过点C作CD∥OB;
(2)以点C为圆心,CO的长为半径作弧,交CD于点E;
(3)作射线OE.
所以射线OE就是∠AOB的角平分线.
请回答:小米的作图依据是_______________________
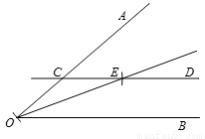
查看答案和解析>>
科目:初中数学 来源:2017届广东省广州市番禺区九年级中考一模数学试卷(解析版) 题型:解答题
如图,已知,在Rt 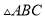 中,斜边
中,斜边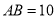 ,
, 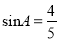 ,点P为边AB上一动点(不与A,B重合),PQ平分
,点P为边AB上一动点(不与A,B重合),PQ平分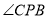 交边BC于点Q,
交边BC于点Q, 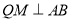 于
于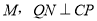 于N.
于N.
(1)当AP=CP时,求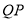 ;
;
(2)若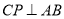 ,求CQ;
,求CQ;
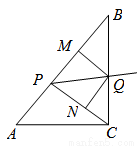
(3)探究:AP为何值时,四边形PMQN与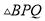 的面积相等?
的面积相等?
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古七年级下学期期中考试数学试卷(解析版) 题型:单选题
计算(-4)2012×(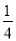 )2011的结果是( )
)2011的结果是( )
A. 4 B. -4 C. 16 D. -16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com