
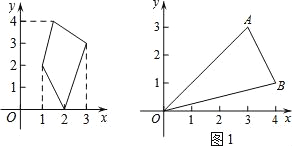
【题目】在平面直角坐标系xOy中,图形W在坐标轴上的投影长度定义如下:设点P(x1,y1),Q(x2,y2)是图形W上的任意两点.若|x1﹣x2|的最大值为m,则图形W在x轴上的投影长度lx=M;若|y1﹣y2|的最大值为n,则图形W在y轴上的投影长度ly=n.如图1,图形W在x轴上的投影长度lx=|3﹣1|=2;在y轴上的投影长度ly=|4﹣0|=4.
(1)已知点A(3,3),B(4,1).如图2所示,若图形W为△OAB,则lx ,ly .
(2)已知点C(4,0),点D在直线y=2x+6上,若图形W为△OCD.当lx=ly时,求点D的坐标.
(3)若图形W为函数y=x2(a≤x≤b)的图象,其中0≤a<b.当该图形满足lx=ly≤1时,请直接写出a的取值范围.
【答案】(1)4;3;(2)(﹣![]() ,
,![]() )或(﹣10,﹣14);(3)0≤a<
)或(﹣10,﹣14);(3)0≤a<![]() .
.
【解析】
(1)确定出点A在y轴的投影的坐标、点B在x轴上投影的坐标,于是可求得问题的答案;
(2)过点P作PD⊥x轴,垂足为P.设D(x,2x+6),则PD=2x+6.PC=4-x,然后依据lx=ly,列方程求解即可;
(3)设A(a,a2)、B(b,b2).分别求得图形在y轴和x轴上的投影,由lx=ly可得到b+a=1,然后根据0≤a<b可求得a的取值范围.
解:(1)∵A(3,3),
∴点A在y轴上的正投影的坐标为(0,3).
∴△OAB在y轴上的投影长度ly=3.
∵B(4,1),
∴点B在x轴上的正投影的坐标为(4,0).
∴△OAB在x轴上的投影长度lx=4.
故答案为:4;3.
(2)如图1所示;过点P作PD⊥x轴,垂足为P.
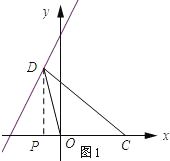
设D(x,2x+6),则PD=2x+6.
∵PD⊥x轴,
∴P(x,0).
∴PC=4﹣x.
∵lx=ly,
∴2x+6=4﹣x,解得;x=﹣![]() .
.
∴D(﹣![]() ,
,![]() ).
).
如图2所示:过点D作DP⊥x轴,垂足为P.
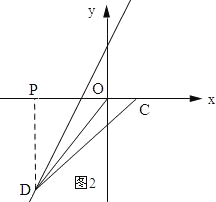
设D(x,2x+6),则PD=﹣2x﹣6.
∵PD⊥x轴,
∴P(x,0).
∴PC=4﹣x.
∵lx=ly,
∴﹣2x﹣6=4﹣x,解得;x=﹣10.
∴D(﹣10,﹣14).
综上所述,点D的坐标为(﹣![]() ,
,![]() )或(﹣10,﹣14).
)或(﹣10,﹣14).
(3)如图3所示:
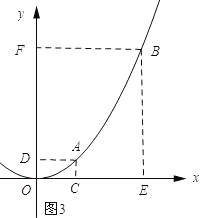
设A(a,a2)、B(b,b2).则CE=b﹣a,DF=b2﹣a2=(b+a)(b﹣a).
∵lx=ly,
∴(b+a)(b﹣a)=b﹣a,即(b+a﹣1)(b﹣a)=0.
∵b≠a,
∴b+a=1.
又∵0≤a<b,
∴a+a<1,
∴0≤a<![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD的各顶点坐标分别为A(1,0),B(2,0),C(2,2),D(0,1);四边形BFGH的各顶点坐标分别为F(4,0),G(4,4),H(0,2).则下列说法正确的是( )
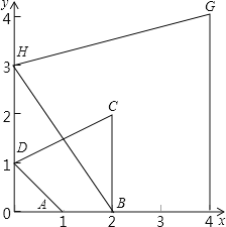
A.四边形ABCD与四边形BFGH相似但不位似
B.四边形ABCD与四边形BFGH位似但不相似
C.四边形ABCD与四边形BFGH位似,且位似比为l:![]()
D.四边形ABCD与四边形BFGH位似,且位似比为l:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车库出口处设置有“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的连接点,当车辆经过时,栏杆AEF升起后的位置如图1所示(图2为其几何图形).其中AB⊥BC,DC⊥BC,EF∥BC,∠EAB=150°,AB=AE=1.2m,BC=2.4m.
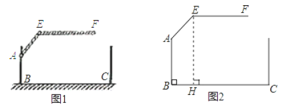
(1)求图2中点E到地面的高度(即EH的长.![]() ≈1.73,结果精确到0.01m,栏杆宽度忽略不计);
≈1.73,结果精确到0.01m,栏杆宽度忽略不计);
(2)若一辆厢式货车的宽度和高度均为2m,这辆车能否驶入该车库?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
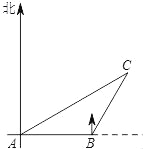
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4).
ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4).
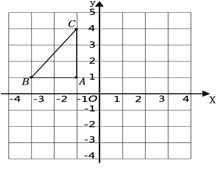
(1)画出△ABC关于y轴对称的图形;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市准备购进甲、乙两种品牌的文具盒,甲、乙两种玩具盒的进价和售价如下表,预计购进乙品牌文具盒的数量y(个)与甲品牌玩具盒数量x(个)之间的函数关系如图所示.
甲 | 乙 | |
进价(元) | 15 | 30 |
售价(元) | 20 | 38 |
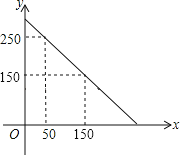
(1)y与x之间的函数关系式是 ;
(2)若超市准备用不超过6000元购进甲、乙两种文具盒,则至少购进多少个甲种文具盒?
(3)在(2)的条件下,写出销售所得的利润W(元)与x(个)之间的关系式,并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8cm,则AB=_____ cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com