
【题目】某超市准备购进甲、乙两种品牌的文具盒,甲、乙两种玩具盒的进价和售价如下表,预计购进乙品牌文具盒的数量y(个)与甲品牌玩具盒数量x(个)之间的函数关系如图所示.
甲 | 乙 | |
进价(元) | 15 | 30 |
售价(元) | 20 | 38 |
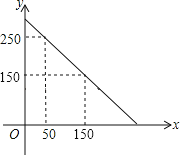
(1)y与x之间的函数关系式是 ;
(2)若超市准备用不超过6000元购进甲、乙两种文具盒,则至少购进多少个甲种文具盒?
(3)在(2)的条件下,写出销售所得的利润W(元)与x(个)之间的关系式,并求出获得的最大利润.
【答案】(1) y=-x+300;(2) 至少购进多200甲种文具盒;(3)W=-3x+2400,最大利润1800元
【解析】
(1)利用待定系数法即可解决问题;
(2)构建不等式即可解决问题;
(3)根据一次函数,利用一次函数的性质即可解决问题;
(1)设y=kx+b,把(50,250),(150,150)代入得:
![]() ,
,
解得![]() ,
,
∴y=-x+300.
故答案是:y=-x+300.
(2)由题意:15x+30(-x+300)≤6000,
解得x≥200,
∴至少购进多200甲种文具盒.
(3)w=5x+8(-x+300)=-3x+2400,
∵y随x的增大而减少,x≥200,
∴x=200时,y有最大值,最大值=1800(元).


科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣2.8+(﹣3.6)+(+3)﹣(﹣3.6)
(2)(﹣4)2010×(﹣0.25)2009+(﹣12)×(![]() ﹣
﹣![]() +
+![]() )
)
(3)13°16'×5﹣19°12'÷6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、点D、线段BC,请用无刻度的直尺和圆规按下列要求与步骤画图:
(1)画直线AB;
(2)画射线DA;
(3)连接CD;
(4)延长线段BC至点E,使得CE=BC(请保留作图痕迹);
(5)在四边形ABCD内找一点O,使得OA+OB+OC+OD的值最小.
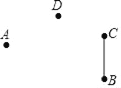
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣4x﹣m2=0
(1)求证:该方程有两个不等的实根;
(2)若该方程的两个实数根x1、x2满足x1+2x2=9,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,定义直线
中,定义直线 ![]() 与双曲线
与双曲线 ![]() 的交点
的交点 ![]() (m、n为正整数)为 “双曲格点”,双曲线
(m、n为正整数)为 “双曲格点”,双曲线 ![]() 在第一象限内的部分沿着竖直方向平移或以平行于
在第一象限内的部分沿着竖直方向平移或以平行于 ![]() 轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.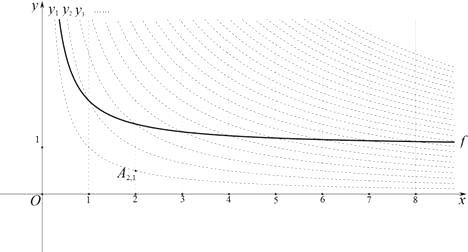
(1)①“双曲格点” ![]() 的坐标为;
的坐标为;
②若线段 ![]() 的长为1个单位长度,则n=;
的长为1个单位长度,则n=;
(2)图中的曲线 ![]() 是双曲线
是双曲线 ![]() 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点 ![]() ,则
,则 ![]() 的解析式为 y=;
的解析式为 y=;
(3)画出双曲线 ![]() 的“派生曲线”g(g与双曲线
的“派生曲线”g(g与双曲线 ![]() 不重合),使其经过“双曲格点”
不重合),使其经过“双曲格点” ![]() 、
、 ![]() 、
、 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com