
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

【答案】(1)59°40′; 29°20′; 60°40′; (2)2α;
(3)360°-2α.
【解析】
(1)根据∠BOC=∠AOB-∠AOC进行计算即可,
由OC平分∠MOB得∠BOM=2∠BOC,则∠AOM=∠BOM-∠AOB,
∠BON=180°-∠BOM,代入计算即可得出答案;
(2)仿照(1)中方法,先求出∠BOC,再求得∠BOM,最后再代入∠BON=180°-∠BOM化简即可;
(3)由图可知∠BOC=∠AOC-∠AOB,然后由角平分线定义得∠BOM=2∠BOC,最后代入∠BON=180°-∠BOM化简即可得出答案.
解:(1)∠BOC=∠AOB-∠AOC
=90°-30°20′
=59°40′,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2×59°40′=119°20′,
∴∠AOM=∠BOM-∠AOB
=119°20′-90°
=29°20′,
∠BON=180°-∠BOM
=180°-119°20′
=60°40′.
故答案为:59°40′,29°20′,60°40′;
(2)∠BOC=∠AOB-∠AOC=90°-α,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2(90°-α)=180°-2α,
∴∠BON=180°-∠BOM
=180°-(180°-2α)
=2α.
故答案为:2α;
(3)由图可知∠BOC=∠AOC-∠AOB=α-90°,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2(α-90°)= 2α-180°,
∴∠BON=180°-∠BOM
=180°-(2α-180°)
=360°-2α.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 | a | b | 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出a,b的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
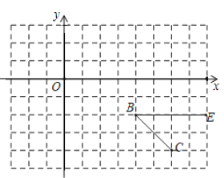
【题目】如图,平面直角坐标系中,![]()
![]() 轴,点
轴,点![]() 从原点
从原点![]() 出发在
出发在![]() 轴上以
轴上以![]() 单位/秒的速度向
单位/秒的速度向![]() 轴的正方向运动,运动的时间为
轴的正方向运动,运动的时间为![]() 秒.
秒.![]() 平分
平分![]() . (提示:
. (提示:![]() 中,
中,![]() ,若
,若![]() 则
则![]() ,反之亦然)
,反之亦然)
(1)当![]() 时,
时,![]() ;
;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() 点运动的时间
点运动的时间![]() ;
;
(3)当![]() 时,求
时,求![]() 的度数(用含
的度数(用含![]() 的式子表示,且不含绝对值).
的式子表示,且不含绝对值).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市准备购进甲、乙两种品牌的文具盒,甲、乙两种玩具盒的进价和售价如下表,预计购进乙品牌文具盒的数量y(个)与甲品牌玩具盒数量x(个)之间的函数关系如图所示.
甲 | 乙 | |
进价(元) | 15 | 30 |
售价(元) | 20 | 38 |
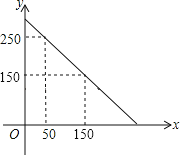
(1)y与x之间的函数关系式是 ;
(2)若超市准备用不超过6000元购进甲、乙两种文具盒,则至少购进多少个甲种文具盒?
(3)在(2)的条件下,写出销售所得的利润W(元)与x(个)之间的关系式,并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣![]() x+
x+![]() 与边AB,BC分别相交于点M,N,函数y=
与边AB,BC分别相交于点M,N,函数y=![]() (x>0)的图象过点M.
(x>0)的图象过点M.
(1)试说明点N也在函数y=![]() (x>0)的图象上;
(x>0)的图象上;
(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═![]() (x>0)的图象仅有一个交点时,求直线M'N′的解析式.
(x>0)的图象仅有一个交点时,求直线M'N′的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨2000元的原料运回工厂,制成每吨5000元的产品运到B地,已知公路运价为2元/(吨·千米),铁路运价为1.5元/(吨·千米),且这两次运输共支出公路运输费14000元,铁路运输费87000元.

(1)求:该工厂从A地购买了多少吨原料?制成运往B地的产品多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,双曲线
中,双曲线 ![]() 与直线
与直线 ![]() 交于点A(3,1).
交于点A(3,1).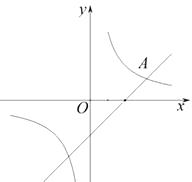
(1)求直线和双曲线的解析式;
(2)直线 ![]() 与x轴交于点B,点P是双曲线
与x轴交于点B,点P是双曲线 ![]() 上一点,过点P作直线PC∥x轴,交y轴于点C,交直线
上一点,过点P作直线PC∥x轴,交y轴于点C,交直线 ![]() 于点D.若DC=2OB,直接写出点
于点D.若DC=2OB,直接写出点 ![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com