【题目】如图，C，D，E将线段AB分成2：3：4：5四部分，M，P，Q，N分别是AC，CD，DE，EB的中点，且MN＝21，求线段PQ的长度．
黄冈创优卷系列答案科目：初中数学 来源： 题型：
【题目】阅读下面文字，然后回答问题．
大家知道
是无理数，而无理数是无限不循环小数，所以的小数部分我们不可能全部写出来，由于的整数部分是1，将 减去它的整数部分，差就是它的小数部分，因此的小数部分可用﹣1表示．
由此我们得到一个真命题：如果＝x+y，其中x是整数，且0＜y＜1，那么x＝1，y＝﹣1．
请解答下列问题：
（1）如果
＝a+b，其中a是整数，且0＜b＜1，那么a＝ ，b＝ ；
（2）如果﹣＝c+d，其中c是整数，且0＜d＜1，那么c＝ ，d＝ ；
（3）已知2+＝m+n，其中m是整數，且0＜n＜1，求|m﹣n|的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管（ ）根．
A. 2 B. 4 C. 5 D. 无数
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，
为坐标原点，点
的坐标为
，点
坐标为
，
、
、
满足
．
（1）若没有平方根，判断点在第几象限并说明理由；
（2）若点到
轴的距离是点到轴距离的
倍，求点的坐标；
（3）点
的坐标为
，
的面积是
面积的
倍，求点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知：∠MON=30°，点A1、A2、A3、…在射线ON上，点B1、B2、B3、…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形，若OA1=1，则△A9B9A10的边长为（ ）
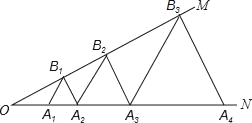
A. 32 B. 64 C. 128 D. 256
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）﹣2.8+（﹣3.6）+（+3）﹣（﹣3.6）
（2）（﹣4）2010×（﹣0.25）2009+（﹣12）×（
﹣
+
）
（3）13°16'×5﹣19°12'÷6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD平分∠BAC，∠C=90°,DE⊥AB于点E，点F在AC上，BD=DF.
（1）求证：CF=EB.
（2）若AB=12，AF=8，求CF的长。
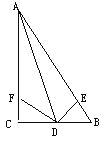
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=
则∠BOC=_______，∠AOM=_______，∠BON=_________；
(2)若∠AOC=
则∠BON=_______(用含有
的式子表示)；
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变，若∠AOC=(为钝角),求∠BON的度数(用含的式子表示).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知四边形ABCD为等腰梯形，AD∥BC，AB=CD，AD= 
，E为CD中点，连接AE，且AE=2 
，∠DAE=30°，作AE⊥AF交BC于F，则BF=（ ）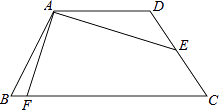
A.1
B.3﹣
C.
﹣1
D.4﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
