
【题目】计算:
(1)﹣2.8+(﹣3.6)+(+3)﹣(﹣3.6)
(2)(﹣4)2010×(﹣0.25)2009+(﹣12)×(![]() ﹣
﹣![]() +
+![]() )
)
(3)13°16'×5﹣19°12'÷6
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.
(1)请写出二次函数y=2(x﹣2)2+1的“对称二次函数”;
(2)已知关于x的二次函数y1=x2﹣3x+1和y2=ax2+bx+c,若y1﹣y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当﹣3≤x≤3时,y2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=80°,OM是∠AOB的平分线,∠BOC=20°,ON是∠BOC的平分线,则∠MON的度数为( )
A.30° B.40° C.50° D.30°或50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市准备购进甲、乙两种品牌的文具盒,甲、乙两种玩具盒的进价和售价如下表,预计购进乙品牌文具盒的数量y(个)与甲品牌玩具盒数量x(个)之间的函数关系如图所示.
甲 | 乙 | |
进价(元) | 15 | 30 |
售价(元) | 20 | 38 |
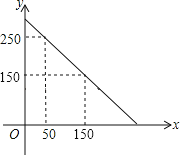
(1)y与x之间的函数关系式是 ;
(2)若超市准备用不超过6000元购进甲、乙两种文具盒,则至少购进多少个甲种文具盒?
(3)在(2)的条件下,写出销售所得的利润W(元)与x(个)之间的关系式,并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为 . 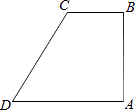
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com