
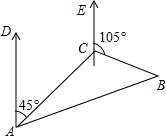
 某货船在索马里海域航行中遭遇海盗袭击,发出呼救信号,我海军护航舰在A处获悉后,立即测出该船在方位角45°,距离10海里的C处,并测得该船正沿方位角105°的方向,以每小时10海里的速度向前行驶,我海军护航舰立即以每小时10$\sqrt{3}$海里的速度前去营救,求护航舰的舰向和靠近货船所需的时间.
某货船在索马里海域航行中遭遇海盗袭击,发出呼救信号,我海军护航舰在A处获悉后,立即测出该船在方位角45°,距离10海里的C处,并测得该船正沿方位角105°的方向,以每小时10海里的速度向前行驶,我海军护航舰立即以每小时10$\sqrt{3}$海里的速度前去营救,求护航舰的舰向和靠近货船所需的时间. 分析 过点B作BM⊥AC的延长线于点M,设所需时间为t小时,则AB=10$\sqrt{3}$t,CB=10t,先根据∠DAC、∠ECB的度数求出∠BCM,从而求出CM=5t,BM=5$\sqrt{3}$t,
再根据AB=2BM求出∠BAM的度数,再求出∠BAD的度数得出护航舰的舰向,根据勾股定理得出AM2+BM2=AB2,再代入得出(10+5t)2+(5$\sqrt{3}$t)2=(10$\sqrt{3}$t)2,最后求出t的值即可.
解答 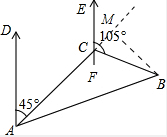 解:过点B作BM⊥AC的延长线于点M,
解:过点B作BM⊥AC的延长线于点M,
设所需时间为t小时,则AB=10$\sqrt{3}$t,CB=10t,
∵∠DAC=45°,
∴∠ACF=45°,
∵∠ECB=105°,
∴∠BCF=75°,
∴∠ACB=45+75=120°,
∴∠BCM=60°,
∴CM=5t,BM=5$\sqrt{3}$t,
∴AM=10+5t,AB=2BM,
∴∠BAM=30°,
∴∠BAD=75°,
∴护航舰的舰向为北偏东75°,
在Rt△ABF中,
∵AM2+BM2=AB2,
∴(10+5t)2+(5$\sqrt{3}$t)2=(10$\sqrt{3}$t)2,
∴t=1或t=-$\frac{1}{2}$(舍去),
∴护航舰靠近货船所需的时间为1小时;
答:护航舰的舰向为北偏东75°,靠近货船所需的时间为1小时.
点评 此题考查了解直角三角形的应用,用到的知识点是方向角、锐角三角函数、特殊角的三角函数值,关键是根据题意求出角的度数.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | -$\frac{3}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
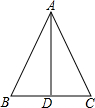 下列条件中能使△ABD≌△ACD的是( )
下列条件中能使△ABD≌△ACD的是( )| A. | AB=AC,∠B=∠C | B. | AB=AC,∠ADB=∠ADC | C. | AB=AC,∠BAD=∠CAD | D. | BD=CD,∠BAD=∠CAD |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com