
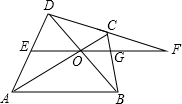
 如图,四边形ABCD中,AC、BD交于O,过O作直线EF∥AB,交AD、BC于E,G,交DC延长线于F,求证:FO2=FG•FE.
如图,四边形ABCD中,AC、BD交于O,过O作直线EF∥AB,交AD、BC于E,G,交DC延长线于F,求证:FO2=FG•FE. 分析 延长AE,BC交于点K,由于EH∥BC,于是得到△DEF∽△DKC,△DEG∽△DKB,推出$\frac{FG}{OF}=\frac{BK}{AK}$,由于EH∥BC,于是得到△AEG∽△AKC,△AEH∽△AKB,推出$\frac{OF}{EF}=\frac{BK}{AK}$,等量代换得到$\frac{FG}{OF}=\frac{OF}{EF}$,于是得到结论.
解答 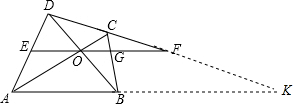 解:延长DF,AB交于点K,
解:延长DF,AB交于点K,
∵EF∥AB,
∴△CFG∽△CKB,△CFO∽△CAK,
∴$\frac{FG}{BK}=\frac{CF}{CK}$,$\frac{OF}{AK}=\frac{CF}{CK}$,
∴$\frac{FG}{BK}=\frac{OF}{AK}$,
∴$\frac{FG}{OF}=\frac{BK}{AK}$,
∵EF∥AB,
∴△DFO∽△DBK,△DEF∽△DAK,
∴$\frac{OF}{BK}=\frac{DF}{DK}$,$\frac{EF}{AK}=\frac{DF}{DK}$,
∴$\frac{OF}{BK}=\frac{EF}{AK}$,
∴$\frac{OF}{EF}=\frac{BK}{AK}$,
∴$\frac{FG}{OF}=\frac{OF}{EF}$,
∴FO2=FG•FE.
点评 本题考查了相似三角形的判定和性质,正确的作出辅助线构造相似三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
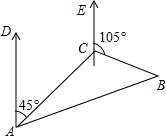 某货船在索马里海域航行中遭遇海盗袭击,发出呼救信号,我海军护航舰在A处获悉后,立即测出该船在方位角45°,距离10海里的C处,并测得该船正沿方位角105°的方向,以每小时10海里的速度向前行驶,我海军护航舰立即以每小时10$\sqrt{3}$海里的速度前去营救,求护航舰的舰向和靠近货船所需的时间.
某货船在索马里海域航行中遭遇海盗袭击,发出呼救信号,我海军护航舰在A处获悉后,立即测出该船在方位角45°,距离10海里的C处,并测得该船正沿方位角105°的方向,以每小时10海里的速度向前行驶,我海军护航舰立即以每小时10$\sqrt{3}$海里的速度前去营救,求护航舰的舰向和靠近货船所需的时间.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
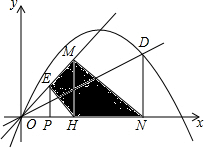 如图,在平面直角坐标系中,等腰直角三角形OMN的斜边ON在x轴上,顶点M的坐标为(3,3),MH为斜边上的高.过N点垂直于x轴的直线与抛物线y=-$\frac{1}{4}{x}^{2}+nx$交于点D,直线OD的解析式为y=$\frac{1}{2}x$.点P(x,0)是x轴上一动点,过点P作y轴的平行线,交射线OM于点E.
如图,在平面直角坐标系中,等腰直角三角形OMN的斜边ON在x轴上,顶点M的坐标为(3,3),MH为斜边上的高.过N点垂直于x轴的直线与抛物线y=-$\frac{1}{4}{x}^{2}+nx$交于点D,直线OD的解析式为y=$\frac{1}{2}x$.点P(x,0)是x轴上一动点,过点P作y轴的平行线,交射线OM于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
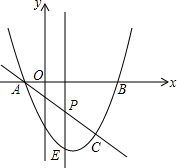 如图,抛物线y=x2-2x-3与x轴交A,B两点(A点在B点左侧),直线l与抛物线交于A,C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交A,B两点(A点在B点左侧),直线l与抛物线交于A,C两点,其中C点的横坐标为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
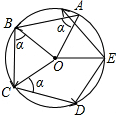 如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?
如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com