

分析 (1)结论∠BCG+∠DCE=180根据周角的定义即可证明.
(2)过点E作EM⊥DC于M点,过点G作GN⊥BC交BC的延长线于N点,先证明△CME≌△CNG求得EM=GN,然后根据三角形的面积公式即可证得;
猜想论证:①过点E作EM⊥DC于M,过点B作BN⊥GC交GC的延长线于点N,根据旋转的性质得出CE=CB,CG=CD,进而得出∠1=∠3,从而得出△CME≌△CNB,通过全等得出EM=BN,然后根据三角形的面积公式即可证得;
②先根据AD∥CE得出∠DAC=∠ACE=30°,进而得出∠BAD=90°,DM=$\frac{1}{2}$AD,BN⊥EC,然后通过解直角三角函数求得AD,从而得出DM,最后根据三角形面积公式和已知条件得出PN=DM,即可求得CP的长;
解答 (1)解:如图1中,∵四边形ABCD、EFGC都是正方形,
∴∠BCD=∠ECG=90°,
∵∠BCG+∠BCD+∠DCE+∠ECG=360°,
∴∠BCG+∠ECD=180°,
故答案为180°
(2)证明:如图1,过点E作EM⊥DC于M点,过点G作GN⊥BC交BC的延长线于N点,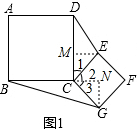
∴∠EMC=∠N=90°,
∵四边形ABCD和四边形ECGF为正方形,
∴∠BCD=∠DCN=∠ECG=90°,CB=CD,CE=CG,
∴∠1=90°-∠2,∠3=90°-∠2,
∴∠1=∠3.
在△CME和△CNG中,
$\left\{\begin{array}{l}{∠EMC=∠GNC}\\{∠1=∠3}\\{EC=CG}\end{array}\right.$,
∴△CME≌△CNG(ASA).
∴EM=GN.
又∵S1=$\frac{1}{2}$CD•EM,S2=$\frac{1}{2}$CB•GN,
∴S1=S2;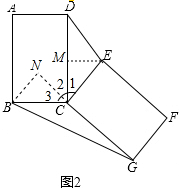 故答案为S1=S2.
故答案为S1=S2.
猜想论证:①猜想:S1=S2,
证明:如图2,过点E作EM⊥DC于M,过点B作BN⊥GC交GC的延长线于点N,
∴∠EMC=∠N=90°,
∵矩形CGFE由矩形ABCD旋转得到的,
∴CE=CB,CG=CD,
∵∠ECG=∠ECN=∠BCD=90°,
∴∠1=90°-∠2,∠3=90°-∠2,∴∠1=∠3.
在△CME和△CNB中
$\left\{\begin{array}{l}{∠EMC=∠BNC}\\{∠1=∠3}\\{EC=CG}\end{array}\right.$,
∴△CME≌△CNB(ASA).
∴EM=BN.
又∵S1=$\frac{1}{2}$CD•EM,S2=$\frac{1}{2}$CG•BN,
∴S1=S2; 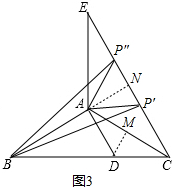
②CP=$\frac{10}{3}$$\sqrt{3}$cm或$\frac{20}{3}$$\sqrt{3}$ cm.
理由:如图3,作DM⊥AC于M,延长BA,交EC于N,
∵AB=AC=10cm,∠B=30°,
∴∠ACB=∠ABC=30°,
∴∠BAC=120°,
根据对折的性质,∠ACE=∠ACB=30°,
∵AD∥CE,
∴∠DAC=∠ACE=30°,
∴∠BAD=90°,DM=$\frac{1}{2}$AD,
∴BN⊥EC,
∵AD=tan∠ABD•AB,AB=10cm,
∴AD=tan30°×10=$\frac{10}{3}$$\sqrt{3}$,
∴DM=$\frac{1}{2}$×$\frac{10}{3}$$\sqrt{3}$=$\frac{5}{3}$$\sqrt{3}$,
∵S△ABP=$\frac{1}{2}$AB•PN,S△ADC=$\frac{1}{2}$AC•DM,S△ABP=S△ADC,AB=AC,
∴PN=DM=$\frac{5}{3}$$\sqrt{3}$,
在RT△ANC中∠ACN=30°,AC=10cm,
∴NC=cos∠ACN•AC=cos30°×10=5 $\sqrt{3}$,
∵在EC上到N的距离等于 $\frac{5}{3}$$\sqrt{3}$的点有两个,
∴P′C=$\frac{10}{3}$$\sqrt{3}$cm,P″C=$\frac{20}{3}$$\sqrt{3}$cm,
∴CP的长为:$\frac{10}{3}$$\sqrt{3}$cm或 $\frac{20}{3}$$\sqrt{3}$cm.
点评 本题考查了正方形的性质,矩形的性质,旋转的性质,全等三角形的判定和性质,平行线的性质,直角三角函数的应用等,找出两个三角形的高的关系是本题的关键,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABD≌△CDB,下面四个结论中不正确的是( )
如图,△ABD≌△CDB,下面四个结论中不正确的是( )| A. | △ABD和△CDB的面积相等 | B. | △ABD和△CDB的周长相等 | ||
| C. | ∠A+∠ABD=∠C+∠CBD | D. | AD∥BC,且AD=BC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知a∥b,三角形的直角顶点在直线a上,已知∠1=25°18'27'',则∠2的度数是( )
如图,已知a∥b,三角形的直角顶点在直线a上,已知∠1=25°18'27'',则∠2的度数是( )| A. | 25°18'27'' | B. | 64° 41'33'' | C. | 74°41'33'' | D. | 64° 41'43'' |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
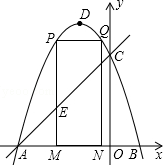 如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com