
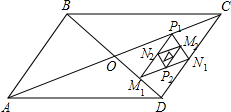
 如图,平行四边形ABCD的面积是16,对角线AC、BD相交于点O,点M1、N1、P1分别为线段OD、DC、CO的中点,顺次连接M1N1、N1 P1、P1M1得到第一个△P1M1N1,面积为S1,分别取M1N1、N1P1、P1M1三边的中点P2、M2、N2,得到第二个△P2M2N2,面积记为S2,如此继续下去得到第n个△PnMnNn,面积记为Sn,则Sn-Sn-1=________.(用含n的代数式表示,n≥2,n为整数)
如图,平行四边形ABCD的面积是16,对角线AC、BD相交于点O,点M1、N1、P1分别为线段OD、DC、CO的中点,顺次连接M1N1、N1 P1、P1M1得到第一个△P1M1N1,面积为S1,分别取M1N1、N1P1、P1M1三边的中点P2、M2、N2,得到第二个△P2M2N2,面积记为S2,如此继续下去得到第n个△PnMnNn,面积记为Sn,则Sn-Sn-1=________.(用含n的代数式表示,n≥2,n为整数)
 =1,依次往下,M2、N2、P2又将△M1N1P1的面积分为相等四分,故S2的面积可求,依此类推即可求出Sn和Sn-1的值,问题得解.
=1,依次往下,M2、N2、P2又将△M1N1P1的面积分为相等四分,故S2的面积可求,依此类推即可求出Sn和Sn-1的值,问题得解. =4,
=4, =1,依次往下,M2、N2、P2又将△M1N1P1的面积分为相等四分,故S2=S△M2N2P2=
=1,依次往下,M2、N2、P2又将△M1N1P1的面积分为相等四分,故S2=S△M2N2P2= S△M1N1P1=4×
S△M1N1P1=4× ×
× =4×
=4× ,
,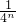 ,
,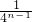 ,
,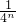 -4×
-4×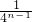 =-
=- .
. .
.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:
 次方程x2-7x+12=0的两个根,且OA>OB.
次方程x2-7x+12=0的两个根,且OA>OB.| OA |
| AB |
| 16 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com