
【题目】如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据.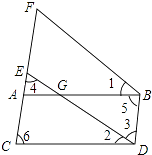
证明:∵∠3=∠4( 已知 )
∴CF∥BD
∴∠5+∠CAB=180°
∵∠5=∠6( 已知 )
∴∠6+∠CAB=180°( 等式的性质 )
∴AB∥CD
∴∠2=∠EGA
∵∠1=∠2( 已知 )
∴∠1=∠EGA( 等量代换 )
∴ED∥FB .
【答案】内错角相等,两直线平行;两直线平行,同旁内角互补;同旁内角互补,两直线平行;两直线平行,同位角相等;同位角相等,两直线平行
【解析】证明:∵∠3=∠4(已知),
∴CF∥BD(内错角相等,两直线平行),
∴∠5+∠CAB=180°(两直线平行,同旁内角互补).
∵∠5=∠6(已知),
∴∠6+∠CAB=180°(等式的性质),
∴AB∥CD(同旁内角互补,两直线平行),
∴∠2=∠EGA(两直线平行,同位角相等).
∵∠1=∠2(已知),
∴∠1=∠EGA(等量代换),
∴ED∥FB(同位角相等,两直线平行).
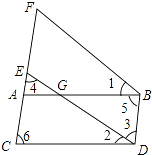
所以答案是:内错角相等,两直线平行;两直线平行,同旁内角互补;同旁内角互补,两直线平行;两直线平行,同位角相等;同位角相等,两直线平行.
【考点精析】利用平行线的判定与性质对题目进行判断即可得到答案,需要熟知由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A,G,H,D且∠1=∠2,∠B=∠C 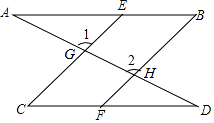
(1)找出图中相互平行的线,说说它们之间为什么是平行的;
(2)证明:∠A=∠D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某织布厂有 150名工人,为了提高经济效益,增设制衣项目,已知每人每天能织布30m,或利用所织布制衣 4 件,制衣一件需要布 1.5m,将布直接出售,每米布可获利 2 元,将布制成衣后出售,每件可获利 25 元,若每名工人只能做一项工作,且不计其他因素,设安排 x 名工人制衣.
(1)一天中制衣所获利润 元(用含 x 的式表示);
(2)一天中销售剩余的布所获利润为 元(用含 x 的式表示);
(3)一天当中安排 名工人制衣时,所获利润为 13712 元;
(4)一年按 300 天计算,一年中这个工厂所获利润最大值为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com