
【题目】如图,![]() 的对角线
的对角线![]() 、
、![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() 其中正确的个数有( )
其中正确的个数有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】C
【解析】
求得∠ADB=90°,即AD⊥BD,即可得到SABCD=ADBD;依据∠CDE=60°,∠BDE=30°,可得∠CDB=∠BDE,进而得出DB平分∠CDE;依据Rt△AOD中,AO>AD,即可得到AO>DE;依据OE是△ABD的中位线,即可得到![]() 。
。
解:∵∠BAD=∠BCD=60°,∠ADC=120°,DE平分∠ADC,
∴∠ADE=∠DAE=60°=∠AED,
∴△ADE是等边三角形,
![]()
∴E是AB的中点,
∴DE=BE,
![]()
∴∠ADB=90°,即AD⊥BD,
∴SABCD=ADBD,故①正确;
∵∠CDE=60°,∠BDE=30°,
∴∠CDB=∠BDE,
∴DB平分∠CDE,故②正确;
∵Rt△AOD中,AO>AD,
∴AO>DE,故③错误;
∵O是BD的中点,E是AB的中点,
∴OE是△ABD的中位线,
∴![]() ,故④正确;
,故④正确;
正确的有3个
故选:C


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:
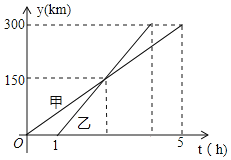
【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.
(1)求乙车离开A城的距离y关于t的函数解析式;
(2)求乙车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的横坐标为3.
的横坐标为3.

(1)直接写出![]() 值________;
值________;
(2)当![]() 取何值时,
取何值时,![]() ?
?
(3)在![]() 轴上有一点
轴上有一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
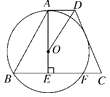
【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是在汛期中防汛指挥部对某河流做的一星期的水位测量(单位:![]() )
)
(注:此河流的警戒水位为![]() ,“+”表示比河流的警戒水位高,“-”表示比河流的警戒水位低)
,“+”表示比河流的警戒水位高,“-”表示比河流的警戒水位低)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位记录 | +2.3 | +0.7 | -5.0 | -1.5 | +3.6 | +1.0 | -2.5 |
(1)本周河流水位最高的一天是______,最低的一天是______,这两天的实际水位分别是_______;
(2)完成下列本周的水位变化表(单位:![]() ),(已知上周末河流的水位比警戒水位低
),(已知上周末河流的水位比警戒水位低![]() .注:规定水位比前一天上升用“+”,比前一天下降用“-”,不升不降用“0”)
.注:规定水位比前一天上升用“+”,比前一天下降用“-”,不升不降用“0”)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化 |
(3)与上周末相比,本周末河流水位上升了还是下降了?变化了多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”.例如,图①中正方形ABCD即为线段BD的“对角线正方形”.如图②,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA﹣AB以5cm/s的速度运动,当点P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).
(1)如图③,借助虚线的小正方形网格,画出线段AB的“对角线正方形”.
(2)当线段PB的“对角线正方形”有两边同时落在△ABC的边上时,求t的值.
(3)当点P沿折线CA﹣AB运动时,求S与t之间的函数关系式.
(4)在整个运动过程中,当线段PB的“对角线正方形”至少有一个顶点落在∠A的平分线上时,直接写出t的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,2![]() ),动点B、C从原点O同时出发,分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动,以点A为圆心,OB的长为半径画圆;以BC为一边,在x轴上方作等边△BCD.设运动的时间为t秒,当⊙A与△BCD的边BD所在直线相切时,t的值为( )
),动点B、C从原点O同时出发,分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动,以点A为圆心,OB的长为半径画圆;以BC为一边,在x轴上方作等边△BCD.设运动的时间为t秒,当⊙A与△BCD的边BD所在直线相切时,t的值为( )

A. ![]() B.
B. ![]() C. 4
C. 4![]() +6 D. 4
+6 D. 4![]() -6
-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种夹克和T恤,夹克每件定价120元,T恤每件定价60元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款.现某客户要到该服装厂购买夹克30件,T恤![]() 件(
件(![]() >30).
>30).
(1)若该客户按方案①购买,需付款 元(用含x的代数式表示);
若该客户按方案②购买,需付款 元(用含x的代数式表示);
(2)若![]() =40,通过计算说明按方案①、方案②哪种方案购买较为合算?
=40,通过计算说明按方案①、方案②哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当![]() =40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并说明理由.
=40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com