
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9.则下列结论错误的是( )
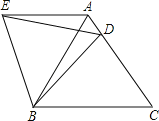
A.AE∥BC
B.△ADE的周长是19
C.△BDE是等边三角形
D.∠ADE=∠BDC
【答案】D
【解析】
试题分析:根据等边三角形的性质得∠ABC=∠C=60°,AC=BC=10,再根据旋转的性质得∠DBE=60°,BD=BE,AE=CD,∠EAB=∠C=60°,则∠EAB=∠ABC=60°,根据平行线的性质可对A选项进行判断;根据等边三角形的判定方法可对C选项进行判断;由于DE=BD=9,则可计算出△ADE的周长=DE+AC=19,于是可对B选项进行判断;先由△BDE是等边三角形得∠BDE=60°,再利用三角形外角性质可得∠ADE=∠DBC,然后根据三角形边角关系得∠BDC>∠DBC,所以∠BDC>∠ADE,于是可对D选项进行判断.
解:∵△ABC为等边三角形,
∴∠ABC=∠C=60°,AC=BC=10,
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠DBE=60°,BD=BE,AE=CD,∠EAB=∠C=60°,
∴∠EAB=∠ABC=60°,
∴AE∥BC;所以A选项的结论正确;
∵∠DBE=60°,BD=BE,
∴△BDE是等边三角形,所以C选项的结论正确;
∴DE=BD=9,
∴△ADE的周长=DE+AE+AD=DE+CD+AD=DE+AC=9+10=19,所以B选项的结论正确;
∵△BDE是等边三角形,
∴∠BDE=60°,
∵∠ADB=∠DBC+∠C,
∴∠ADE+60°=∠DBC+60°,
∴∠ADE=∠DBC,
∵BC>CD,
∴∠BDC>∠DBC,
∴∠BDC>∠ADE,所以D选项的结论错误.
故选D.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】在环境创优活动中,某居民小区要在一块靠墙(墙长25米)的空地上修建一个矩形养鸡场,养鸡场的一边靠墙,如果用60m长的篱笆围成中间有一道篱笆的养鸡场,设养鸡场平行于墙的一边BC的长为x(m),养鸡场的面积为y(m2)
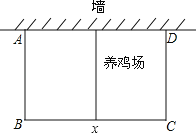
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)养鸡场的面积能达到300m2吗?若能,求出此时x的值,若不能,说明理由;
(3)根据(1)中求得的函数关系式,判断当x取何值时,养鸡场的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠COA=90°,∠COD比∠DOA大28°,且OB是∠COA的平分线.

(1)求∠BOD的度数;
(2)将已知条件中的28°改为32°,则∠BOD= ;
(3)将已知条件中的28°改为n°,则∠BOD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=120°,射线OA绕点O以每秒钟6°的速度逆时针旋转到OP,设射线OA旋转OP所用时间为t秒(t<30).

(1)如图1,直接写出∠BOP= °(用含t的式子表示);
(2)若OM平分∠AOP,ON平分∠BOP.
①当OA旋转到如图1所示OP处,请完成作图并求∠MON的度数;
②当OA旋转到如图2所示OP处,若2∠BOM=3∠BON,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
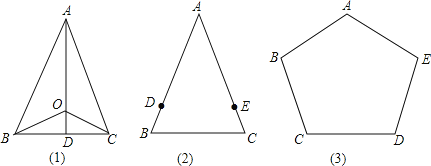
【题目】(1)如图(1),在△ABC,AB=AC,O为△ABC内一点,且OB=OC,求证:直线AO垂直平分BC.以下是小明的证题思路,请补全框图中的分析过程.

(2)如图(2),在△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.请你只用无刻度的直尺画出BC边的垂直平分线(不写画法,保留画图痕迹).
(3)如图(3),在五边形ABCDE中,AB=AE,BC=DE,∠B=∠E,请你只用无刻度的直尺画出CD边的垂直平分线,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是( )

A.甲的速度是4千米/小时
B.乙的速度是10千米/小时
C.甲比乙晚到B地3小时
D.乙比甲晚出发1小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com