
【题目】如图,已知∠COA=90°,∠COD比∠DOA大28°,且OB是∠COA的平分线.

(1)求∠BOD的度数;
(2)将已知条件中的28°改为32°,则∠BOD= ;
(3)将已知条件中的28°改为n°,则∠BOD= .
【答案】(1)14°; (2)16°;(3)(![]() )°.
)°.
【解析】
试题分析:(1)根据已知得出∠DOA+28°+∠DOA=90°,求出∠DOA,根据角平分线求出∠AOB,代入∠BOD=∠AOB﹣∠DOA求出即可;
(2)根据已知得出∠DOA+32°+∠DOA=90°,求出∠DOA,根据角平分线求出∠AOB,代入∠BOD=∠AOB﹣∠DOA求出即可;
(3)根据已知得出∠DOA+n°+∠DOA=90°,求出∠DOA,根据角平分线求出∠AOB,代入∠BOD=∠AOB﹣∠DOA求出即可.
解:(1)∵∠COD比∠DOA大28°,
∴∠COD=∠DOA+28°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+28°+∠DOA=90°,
∴∠DOA=31°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
=![]() ∠AOC
∠AOC
=45°,
∴∠BOD=∠AOB﹣∠DOA
=45°﹣31°
=14°;
(2)∵∠COD比∠DOA大32°,
∴∠COD=∠DOA+32°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+32°+∠DOA=90°,
∴∠DOA=29°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
=![]() ∠AOC
∠AOC
=45°,
∴∠BOD=∠AOB﹣∠DOA
=45°﹣29°
=16°;
故答案为:16°;
(3)∵∠COD比∠DOA大n°,
∴∠COD=∠DOA+n°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+n°+∠DOA=90°,
∴∠DOA=(45﹣![]() )°,
)°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
=![]() ∠AOC
∠AOC
=45°,
∴∠BOD=∠AOB﹣∠DOA
=45°﹣(45﹣![]() )°
)°
=(![]() )°;
)°;
故答案为:(![]() )°.
)°.


科目:初中数学 来源: 题型:
【题目】已知两点P(1,1)、Q(1,-1),若点Q固定,点P绕点Q旋转使线段PQ∥x轴,则此时的点P的坐标是_________________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经统计我市去年共引进世界500强外资企业19家,累计引进外资410000000美元,数字410000000用科学记数法表示为( )
A.41×107 B.4.1×108 C.4.1×109 D.0.41×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )

A.(S.S.S.) B.(S.A.S.) C.(A.S.A.) D.(A.A.S.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AC=BD,∠CAB=∠DBA,试说明:BC=AD

变式1:如图2,AC=BD,BC=AD,试说明:∠CAB=∠DBA;
变式2:如图3,AC=BD,∠C=∠D,试说明:(1)AO=BO(2)CO=DO(3)BC=AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9.则下列结论错误的是( )
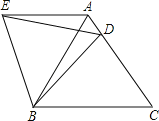
A.AE∥BC
B.△ADE的周长是19
C.△BDE是等边三角形
D.∠ADE=∠BDC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=﹣1是对称轴,有下列判断:①b﹣2a=0;②4a﹣2b+c<0;③a﹣b+c=﹣9a;④若(﹣3,y1),(3,y2)是抛物线上两点,则y1>y2,其中正确的序号是 .
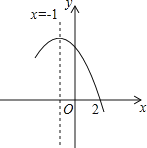
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com