
【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠D=50°,则下列结论:①∠AOE=65°;②OF平分∠BOD;③∠GOE=∠DOF;④∠GOE=25°。其中正确的是:( )
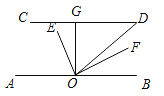
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
科目:初中数学 来源: 题型:
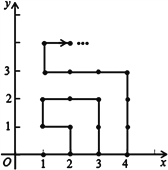
【题目】如图,在平面直接坐标系中,有若干个横坐标分别为整数的点,其顺序按图中(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2016个点的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
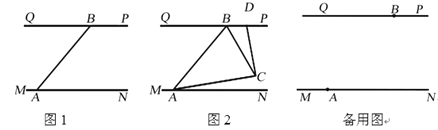
【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a﹣3b|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°
⑴求a、b的值;
⑵若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
⑶如图,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别相交是AB、CD的中点,EF分别交BD、AC于点G、H。求证:OG=OH。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“3.15”期间某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:同一日内,顾客在本商场每消费满200元,就可以在箱子里一次摸出两个球,商场根据两小球所标金额之和返还相应数额的购物券.某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请用树状图或列表求出该顾客所获得的购物券金额不低于30元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com