
| A. | 2$\sqrt{13}$ | B. | 1+3$\sqrt{5}$ | C. | 3+$\sqrt{37}$ | D. | $\sqrt{85}$ |
分析 作BB'垂直于河岸,使BB′等于河宽,连接AB′,与靠近A的河岸相交于M,作MN垂直于另一条河岸,则MN∥BB′且MN=BB′,于是MNBB′为平行四边形,故MB′=BN;根据“两点之间线段最短”,AB′最短,即AM+BN最短,此时AM+BN=AB′.
解答 解:如图,作BB'垂直于河岸,使BB′等于河宽,
连接AB′,与靠近A的河岸相交于M,作MN垂直于另一条河岸,
则MN∥BB′且MN=BB′,
于是MNBB′为平行四边形,故MB′=BN.
根据“两点之间线段最短”,AB′最短,即AM+BN最短.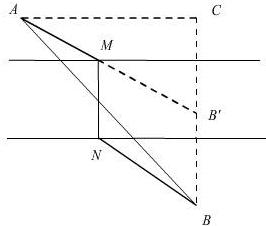
∵AB=10千米,BC=1+3+4=8千米,
∴在RT△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=6,
在RT△AB′C中,B′C=1+3=4千米,
∴AB′=${\sqrt{A{C}^{2}+B′C}}^{2}$=2$\sqrt{13}$千米;
故选A.
点评 本题考查了轴对称---最短路径问题,要利用“两点之间线段最短”,但许多实际问题没这么简单,需要我们将一些线段进行转化,即用与它相等的线段替代,从而转化成两点之间线段最短的问题.目前,往往利用对称性、平行四边形的相关知识进行转化.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:选择题
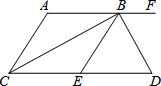 如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论其中错误是( )
如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论其中错误是( )| A. | BC平分∠ABE | B. | AC∥BE | C. | ∠BCD+∠D=90° | D. | ∠DBF=2∠ABC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
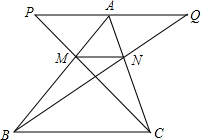 如图,△ABC的顶点A是线段PQ的中点,PQ∥BC,连接PC、QB,分别交AB、AC于M、N,连接MN,若MN=1,BC=3,求线段PQ的长.
如图,△ABC的顶点A是线段PQ的中点,PQ∥BC,连接PC、QB,分别交AB、AC于M、N,连接MN,若MN=1,BC=3,求线段PQ的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
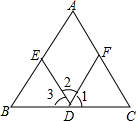 如图,(1)因为∠A=∠BED(已知),
如图,(1)因为∠A=∠BED(已知),查看答案和解析>>
科目:初中数学 来源: 题型:选择题
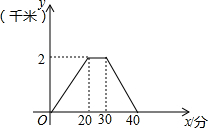 星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )
星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
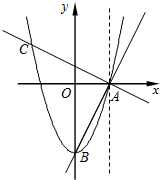 如图,抛物线y=ax2+c经过A(1,0),B(0,-2)两点.连结AB,过点A作AC⊥AB,交抛物线于点C.
如图,抛物线y=ax2+c经过A(1,0),B(0,-2)两点.连结AB,过点A作AC⊥AB,交抛物线于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com