
| A. | c≥-1 | B. | -1≤c<3 | C. | 3<c<8 | D. | -1≤c<8 |
分析 先由抛物线对称轴求出b的值,再根据抛物线与x轴有交点的条件进行列式求解.
解答 解:由抛物线y=x2+bx+c的对称轴为x=1,
∴$-\frac{b}{2a}$=1,$-\frac{b}{2}$=1,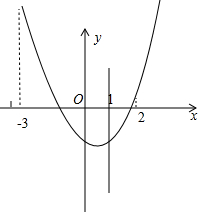
解得:b=-2,
∴x2-bx-c=x2+2x-c,
令y1=x2+2x-c,可求其对称轴为:x=-1,
根据题意,当x=2时,y1>0,x2+2x-c>0,且当x=-1时,y1≤0,x2+2x-c≤0,
或当x=-3时,y>0,9-6-c>0,且当x=-1时,y1≤0,x2+2x-c≤0,
解得:-1≤c<8,或-1≤c<3
综上所述,-1≤c<8.
故选D.
点评 此题主要考查抛物线与x轴的交点问题,会用临界值和对称轴进行分析列式是解题的关键.


科目:初中数学 来源: 题型:解答题
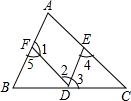 已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.
已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
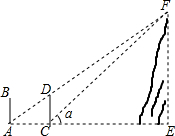 如图,相邻两输电杆AB、CD相距100m,高度都为20m,驾驶员开小汽车到A处时发现前方输电杆CD的顶部与山顶F恰好在一条直线上,小汽车沿平路往前开至C处时看到山顶F的仰角为α=42°,求山顶F的高.(精确到0.1m)
如图,相邻两输电杆AB、CD相距100m,高度都为20m,驾驶员开小汽车到A处时发现前方输电杆CD的顶部与山顶F恰好在一条直线上,小汽车沿平路往前开至C处时看到山顶F的仰角为α=42°,求山顶F的高.(精确到0.1m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com