
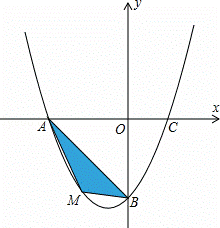
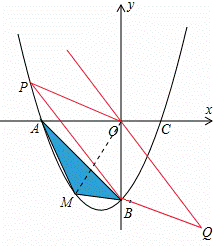
在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.
求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
解:(1)设此抛物线的函数解析式为:
y=ax2+bx+c(a≠0),
将A(﹣4,0),B(0,﹣4),C(2,0)三点代入函数解析式得:
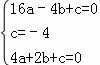
解得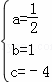 ,
,
所以此函数解析式为:y=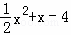 ;
;
(2)∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为:(m,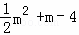 ),
),
∴S=S△AOM+S△OBM﹣S△AOB
=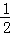 ×4×(﹣
×4×(﹣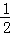 m2﹣m+4)+
m2﹣m+4)+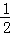 ×4×(﹣m)﹣
×4×(﹣m)﹣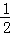 ×4×4
×4×4
=﹣m2﹣2m+8﹣2m﹣8
=﹣m2﹣4m,
=﹣(m+2)2+4,
∵﹣4<m<0,
当m=﹣2时,S有最大值为:S=﹣4+8=4.
答:m=﹣2时S有最大值S=4.
(3)设P(x,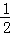 x2+x﹣4).
x2+x﹣4).
当OB为边时,根据平行四边形的性质知PB∥OQ,
∴Q的横坐标的绝对值等于P的横坐标的绝对值,
又∵直线的解析式为y=﹣x,
则Q(x,﹣x).
由PQ=OB,得|﹣x﹣(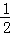 x2+x﹣4)|=4,
x2+x﹣4)|=4,
解得x=0,﹣4,﹣2±2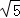 .
.
x=0不合题意,舍去.
如图,当BO为对角线时,知A与P应该重合,OP=4.四边形PBQO为平行四边形则BQ=OP=4,Q横坐标为4,代入y=﹣x得出Q为(4,﹣4).
由此可得Q(﹣4,4)或(﹣2+2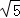 ,2﹣2
,2﹣2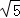 )或(﹣2﹣2
)或(﹣2﹣2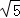 ,2+2
,2+2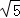 )或(4,﹣4).
)或(4,﹣4).


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
把代数式ax2﹣4ax+4a分解因式,下列结果中正确的是( )
A. a(x﹣2)2 B. a(x+2)2 C. a(x﹣4)2 D. a(x+2)(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
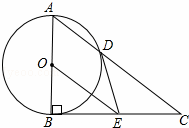
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)试探究线段CD、DE、EO之间的等量关系,并加以证明;
(2)若tanC=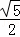 ,DE=2,求AD的长.
,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
某市居民为四川省雅安地震灾区进行募捐,共收到粮食100吨,副食品54吨,现计划租用甲、乙两种货车共8辆将这批货物全部运往雅安,已知一辆甲种货车同时可装运粮食20吨,副食品6吨,一辆乙种货车同时可装运粮食8吨,副食品8吨.
(1)若要将这些货物一次性运到目的地,有几种租用货车的方案?分别是哪几种?
(2)若甲货车租金每辆2000元,乙货车2500元,那么采用哪种租车方案使运费最少呢?最少运费又是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com