解:(1)由直线y=2x+2知:点C(-1,0)、B(0,2);
抛物线y=ax
2-2ax+c过点C(-1,0)、A(5,12),有:
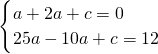
,解得
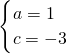
∴抛物线的解析式:y=x
2-2x-3.
(2)由(1)知:OB=2、OC=1;
由题意知:S
△DBO=S
△DCO,则:

×BO×|x
D|=

×CO×|y
D|,即:|y
D|=2|x
D|
∴可以设点D的坐标为:(x,2x)或(x,-2x)(x<-1或x>3),代入抛物线的解析式中,有:
当点D坐标为(x,2x)时,有:x
2-2x-3=2x;解得:x
1=2-

(舍),x
2=2+

;
当点D坐标为(x,-2x)时,有:x
2-2x-3=-2x;解得:x
3=

(舍),x
4=-

;
∴点D的坐标为:(2+

,4+2

)或(-

,2

).
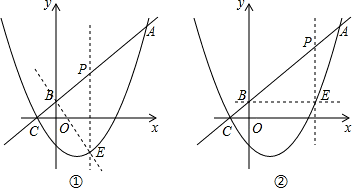
(3)∵PE⊥x轴,且BO⊥CO,
∴PE∥BO,即∠CBO=∠BPE;
若以P、B、E为顶点的三角形与△BOC相似,那么:
①PB⊥BE,如图①;
由于直线BE与直线AC垂直,且过点B(0,2),所以:
直线BE:y=-

x+2;
联立抛物线的解析式,有:
-

x+2=x
2-2x-3,解得:x
1=
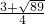
、x
2=
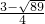
(舍);
将点P横坐标代入直线AC:y=2x+2中,得:y=
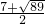
;
∴P
1(
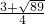
,
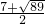
).
②PE⊥BE,如图②;
∵PE∥y轴,且PE⊥BE,
∴BE∥x轴,即 点B、E的纵坐标相同;
令x
2-2x-3=2,解得:x
1=1-

(舍)、x
2=1+

;
将点P横坐标代入直线AC:y=2x+2中,得:y=4+2

;
∴P
2(1+

,4+2

).
综上,存在符合条件的点P,且坐标为(
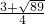
,
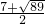
)或(1+

,4+2

).
分析:(1)首先由直线AC的解析式确定点C的坐标,在已知点A坐标的情况下,利用待定系数法可确定抛物线的解析式.
(2)点B、C的坐标易知,那么OB、OC的倍数关系不难求出,那么在△DCO、△DBO中,分别以CO、BO为底进行讨论,若两三角形的面积相等,可确定点D到x轴、y轴距离的比例关系(或边CO、边OB上的高的比例关系),首先根据这个关系设出点D的坐标,再代入(1)的抛物线中即可确定该点的坐标.
(3)由于PE⊥x轴,即PE∥OB,显然有∠BPE=∠CBO,若“以P、B、E为顶点的三角形与△BOC相似”,只需在△BPE中找出一个直角即可,那么分两种情况讨论:
①PB⊥BE,此时直线BE、直线AC的斜率乘积为-1,先确定直线BE的解析式,联立抛物线的解析式后可确定点P的坐标;
②PE⊥BE,由于PE⊥x轴,那么必有BE∥x轴,因此只需将点B的纵坐标代入抛物线的解析式中,进一步可确定点P的坐标;
另外,需要注意的是点P在线段AB上,求出结果后不要忘记根据这个条件对值进行取舍.
点评:该题涉及到利用待定系数法确定函数解析式、三角形面积的解法、函数图象交点坐标的求法以及相似三角形的判定和性质等重点知识;(2)题中,能够由三角形的面积相等得出点D横纵坐标的倍数关系是突破题目的关键;(3)题容易漏解,要注意根据不同情况分类讨论.

 如图,已知直线y=2x+2与x轴交于点C,与y轴交于点B,抛物线y=ax2-2ax+c过点C且与直线y=2x+2交于点A(5,12).
如图,已知直线y=2x+2与x轴交于点C,与y轴交于点B,抛物线y=ax2-2ax+c过点C且与直线y=2x+2交于点A(5,12).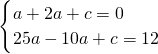 ,解得
,解得 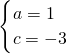
 ×BO×|xD|=
×BO×|xD|= ×CO×|yD|,即:|yD|=2|xD|
×CO×|yD|,即:|yD|=2|xD| (舍),x2=2+
(舍),x2=2+ ;
; (舍),x4=-
(舍),x4=- ;
; ,4+2
,4+2 )或(-
)或(- ,2
,2 ).
). (3)∵PE⊥x轴,且BO⊥CO,
(3)∵PE⊥x轴,且BO⊥CO, x+2;
x+2; x+2=x2-2x-3,解得:x1=
x+2=x2-2x-3,解得:x1=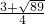 、x2=
、x2=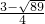 (舍);
(舍);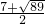 ;
;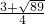 ,
,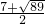 ).
). (舍)、x2=1+
(舍)、x2=1+ ;
; ;
; ,4+2
,4+2 ).
).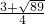 ,
,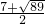 )或(1+
)或(1+ ,4+2
,4+2 ).
).

 天天练口算系列答案
天天练口算系列答案 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 如图,已知直线l1:y=
如图,已知直线l1:y=