
【题目】如图,已知数轴上有![]() 、
、![]() 、
、![]() 三个点,它们表示的数分别是
三个点,它们表示的数分别是![]() ,
,![]() ,10,我们约定点
,10,我们约定点![]() 与点
与点![]() 之间的距离记为
之间的距离记为![]() ,点
,点![]() 与点
与点![]() 之间的距离记为
之间的距离记为![]() .
.
(1)线段![]() 的长度为 ,线段
的长度为 ,线段![]() 的长度为 ;
的长度为 ;
(2)若点![]() 向左运动6个单位长度,则运动后的点表示的数为 ;若点
向左运动6个单位长度,则运动后的点表示的数为 ;若点![]() 向右运动6个单位长度,则运动后的点表示的数为 ;
向右运动6个单位长度,则运动后的点表示的数为 ;
(3)若点![]() 以每秒1个单位长度的速度向左运动,同时点
以每秒1个单位长度的速度向左运动,同时点![]() 和点
和点![]() 分别以每秒3个单位长度和7个单位长度的速度向右运动,设运动时间为
分别以每秒3个单位长度和7个单位长度的速度向右运动,设运动时间为![]() 秒.
秒.
①试用含![]() 的式子分别表示点
的式子分别表示点![]() 、
、![]() 、
、![]() 运动
运动![]() 秒后的位置所对应的数;
秒后的位置所对应的数;
![]()
![]()
![]()
②试探索:![]() 的值是否为定值?若是,请求出其定值;若不是,请说明理由.
的值是否为定值?若是,请求出其定值;若不是,请说明理由.
![]()
【答案】(1)14,20;(2)![]() ,
,![]() ;(3)①
;(3)①![]() ,
,![]() ,
,![]() ;②
;②![]() 的定值为6,详见解析.
的定值为6,详见解析.
【解析】
(1)画出数轴,根据数轴的性质求出线段![]() 的长度和线段
的长度和线段![]() 的长度即可;
的长度即可;
(2)若点![]() 向左运动6个单位后对应的数为
向左运动6个单位后对应的数为![]() ,若点
,若点![]() 向右运动6个单位长度对应的数为
向右运动6个单位长度对应的数为![]() ,分别列出对应的方程求解即可;
,分别列出对应的方程求解即可;
(3)分三种情况:①若点![]() 向左运动
向左运动![]() 秒后对应点所对的数为
秒后对应点所对的数为![]() ;②若点
;②若点![]() 向右运动
向右运动![]() 秒后对应点所对的数为
秒后对应点所对的数为![]() ;③若点
;③若点![]() 向右运动
向右运动![]() 秒后对应点所对的数为
秒后对应点所对的数为![]() ,列出相应方程并求解即可求出A、B、C的值,从而求得AB、BC的值,即可得证
,列出相应方程并求解即可求出A、B、C的值,从而求得AB、BC的值,即可得证![]() 的定值为6.
的定值为6.
(1)如图所示:
![]()
![]() 、
、![]() 、
、![]() 三个点表示的数分别是
三个点表示的数分别是![]() ,
,![]() ,10,
,10,
![]() ,
,
![]() ,
,
故答案为14,20;
(2)若点![]() 向左运动6个单位后对应的数为
向左运动6个单位后对应的数为![]() ,依题意义得:
,依题意义得:
![]() ,
,
解得:![]() ,
,
若点![]() 向右运动6个单位长度对应的数为
向右运动6个单位长度对应的数为![]() ,依题意义得:
,依题意义得:
![]() ,
,
解得:![]() ,
,
故答案为:![]() ,
,![]() ;
;
(3)①若点![]() 向左运动
向左运动![]() 秒后对应点所对的数为
秒后对应点所对的数为![]() ,
,
![]() 个单位长度
个单位长度![]() 秒,
秒,![]() 秒,
秒,
![]() ,
,
![]() ,
,
解得:![]() ;
;
②若点![]() 向右运动
向右运动![]() 秒后对应点所对的数为
秒后对应点所对的数为![]() ,
,
![]() 个单位长度
个单位长度![]() 秒,
秒,![]() 秒,
秒,
![]() ,
,
![]() ,
,
解得:![]() ;
;
③若点![]() 向右运动
向右运动![]() 秒后对应点所对的数为
秒后对应点所对的数为![]() ,
,
![]() 个单位长度
个单位长度![]() 秒,
秒,![]() 秒,
秒,
![]() ,
,
![]() ,
,
解得:![]() ;
;
故答案为:![]() ,
,![]() ,
,![]() ;
;
②定值,理由如下:
![]() ,
,
![]() ,
,
![]() ,
,
即![]() 的定值为6.
的定值为6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 是定长线段
是定长线段![]() 上一定点.点
上一定点.点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,
上,![]() 、
、![]() 两点分别从
两点分别从![]() 、
、![]() 出发,分别以
出发,分别以![]() /
/![]() 、
、![]() /
/![]() 的速度沿直线
的速度沿直线![]() 同时向左运动.
同时向左运动.
(1)若![]() ,当点
,当点![]() 、
、![]() 运动了
运动了![]() ,求
,求![]() 的值;
的值;
(2)若点![]() 、
、![]() 运动时,总有
运动时,总有![]() ,则
,则![]() _____
_____![]() ;
;
(3)在(2)的条件下,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.
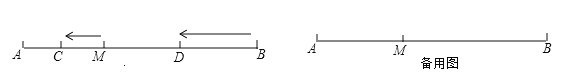
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王叔叔在太原市小店区买了一套商品房,他准备用1万元将地面铺上地砖,这套住宅的建筑平面图(由多个长方形组成)如图所示(图中长度单位:![]() ),请据图解答下列问题.
),请据图解答下列问题.
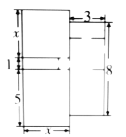
(1)用含![]() 的代数式表示这所住宅的总面积;
的代数式表示这所住宅的总面积;
(2)某公司地砖报价为每平米200元,若![]() ,在现有条件下,王叔叔是否会选择该公司铺地砖?请说明理由.
,在现有条件下,王叔叔是否会选择该公司铺地砖?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
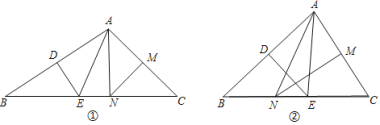
⑴如图①,若![]() ,求
,求![]() 的度数;
的度数;
⑵如图②,若![]() ,求
,求![]() 的度数;
的度数;
⑶若![]()
![]() ,直接写出用
,直接写出用![]() 表示
表示![]() 大小的代数式.
大小的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
已知:如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.
试说明:∠EGF=90°.
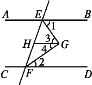
解:因为HG∥AB(已知),
所以∠1=∠3( ).
又因为HG∥CD(已知),
所以∠2=∠4( ).
因为AB∥CD(已知),
所以∠BEF+ =180°( ).
又因为EG平分∠BEF(已知),
所以∠1=![]() ∠ ( ).
∠ ( ).
又因为FG平分∠EFD(已知),
所以∠2=![]() ∠ ( ),
∠ ( ),
所以∠1+∠2=![]() ( + ).
( + ).
所以∠1+∠2=90°.
所以∠3+∠4=90°( ),即∠EGF=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )

A. 17.5° B. 12.5° C. 12° D. 10°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组数中,以a、b、c为边长的三角形不是直角三角形的是( )
A. a=3,b=4,c=5B. a=5,b=12,c=13
C. a=1,b=2,c=![]() D. a=
D. a=![]() ,b=2,c=3
,b=2,c=3
查看答案和解析>>
科目:初中数学 来源: 题型:
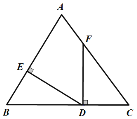
【题目】如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com