练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】王叔叔在太原市小店区买了一套商品房，他准备用1万元将地面铺上地砖，这套住宅的建筑平面图（由多个长方形组成）如图所示（图中长度单位：），请据图解答下列问题．

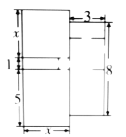
    （1）用含的代数式表示这所住宅的总面积；

    （2）某公司地砖报价为每平米200元，若，在现有条件下，王叔叔是否会选择该公司铺地砖？请说明理由．

    【答案】（1）；（2）王叔叔不会选择该公司铺地砖，见详解

    【解析】

    (1)找到各个长方形和正方形的边长，用代数式表示面积，求得总面积；
    (2)先将x=4代入(1)中得出的式子求出面积，再利用单价×面积即可求得总费用即可得出答案．

    解：（1）这套商品房建筑面积为：

    （2）某公司地砖报价每平米200元，王叔叔不会选择该公司铺地砖

    理由如下：当 时，原式=

    （）

    每平米200元，这套商品房铺地砖需要花费（元）

    王叔叔的1万元不够支付该公司铺地砖费用

    故王叔叔不会选择该公司铺地砖

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某商店在2015年至2017年期间销售一种礼盒。2015年，该商店用3 500元购进了这种礼盒并且全部售完；2017年，这种礼盒的进价比2015年下降了11元/盒，该商店用2 400元购进了与2015年相同数量的礼盒也全部售完，礼盒的售价均为60元/盒．

    (1)2015年这种礼盒的进价是多少元/盒？

    (2)若该商店每年销售这种礼盒所获利润的年增长率相同，问年增长率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是某市民健身广场的平面示意图，它是由6个正方形拼成的长方形，已知中间最小的正方形的边长是1米；

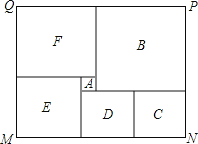
    （1）若设图中最大正方形的边长是米，请用含的代数式分别表示出正方形的边长

    （2）观察图形的特点可知，长方形相对的两边是相等的(即， )请根据以上结论，求出的值

    （3）现沿着长方形广场的四条边铺设下水管道，由甲、乙工程队单独铺设分别需要10天、15天完成，如果两队从同一位置开始，沿相反的方向同时施工2天后，因甲队另有任务，余下的工程由乙队单独施工，还要多少天完成?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB为⊙O的直径，点E在⊙O上，∠EAB的平分线交⊙O于点C，过点C作AE的垂线，垂足为D，直线DC与AB的延长线交于点P．

    （1）判断直线PC与⊙O的位置关系，并说明理由；

    （2）若tan∠P=，AD=6，求线段AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某家电商场计划用9万元从生产厂家购进50台电视机，已知该厂家生产3种不同型号的电视机，出厂价分别为A种每台1500元，B种每台2100元，C种每台2500元．

    （1）若家电商场同时购进两种不同型号的电视机共50台，用去9万元，请你计算一下商场有哪几种进货方案？

    （2）若商场销售一台A种电视机可获利150元，销售一台B种电视机可获利200元，销售一台C种电视机可获利250元，在同时购进两种不同型号的电视机方案中，为了使销售时获利最多，应选择哪种方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践

    如图，根据给出的数轴，解答下面的问题：

    （1）已知点表示的数分别为6，-4，观察数轴，与点距离为5的点所表示的数是 ，两点之间的距离为 ；

    （2）若点到点，点的距离相等，观察数轴并结合所学知识求点表示的数；

    （3）在（2）的条件下，若动点从点出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动时间为秒．则点表示的数是多少（用含字母的式子表示）；当等于多少秒时，之间的距离为3个单位长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知数轴上有、、三个点，它们表示的数分别是，，10，我们约定点与点之间的距离记为，点与点之间的距离记为．

    （1）线段的长度为　　，线段的长度为　　；

    （2）若点向左运动6个单位长度，则运动后的点表示的数为　　；若点向右运动6个单位长度，则运动后的点表示的数为　　；

    （3）若点以每秒1个单位长度的速度向左运动，同时点和点分别以每秒3个单位长度和7个单位长度的速度向右运动，设运动时间为秒．

    ①试用含的式子分别表示点、、运动秒后的位置所对应的数；

    　　　　　　

    ②试探索：的值是否为定值？若是，请求出其定值；若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABF≌△CDE.

    （1）若∠B＝30°，∠DCF＝40°，求∠EFC的度数；

    （2）若BD=10，EF=2，求BF的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

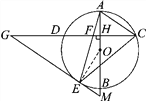
    【题目】如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连接AC，过上一点E作EG∥AC交CD的延长线于点G，连接AE交CD于点F，且EG＝FG，连接CE.

    (1)求证：△ECF∽△GCE；

    (2)求证：EG是⊙O的切线；

    查看答案和解析>>

    同步练习册答案