
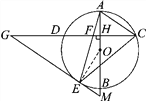
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连接AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG,连接CE.
上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG,连接CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
【答案】(1)证明见解析(2)证明见解析
【解析】(1)由![]() ,得∠ACD=∠AEC,由EG∥AC,得∠G=∠ACD,
,得∠ACD=∠AEC,由EG∥AC,得∠G=∠ACD,
所以,∠FCE=∠ECG,可得三角形相似;
(2)连接OE,由OE=OA可得∠OAE=∠OEA,由GF=GE,得∠GEF=∠GFE=∠AFH,
又∠AFH+∠EAO=90°,可得∠GEF+∠AEO=90°, 即OE⊥GE,故EG是⊙O的切线.
∴![]() ,
,
∴∠ACD=∠AEC,
∵EG∥AC,
∴∠G=∠ACD,
∴∠G=∠AEC,
∵∠FCE=∠ECG,
∴△ECF∽△GCE.
(2)连接OE,
∵CD⊥AB,∴∠AHF=90°,
∴∠AFH+∠FAH=90°,
∵EG=FG,
∴∠GEF=∠GFE.
∵∠GFE=∠AFH,
∴∠GEF=∠AFH,
∵OE=OA,
∴∠OEA=∠OAE,
∴∠GEO=∠GEF+∠FEO=∠AFH+∠FAH=90°,
即OE⊥GE,
∵OE为⊙O的半径,
∴EG是⊙O的切线.


科目:初中数学 来源: 题型:
【题目】王叔叔在太原市小店区买了一套商品房,他准备用1万元将地面铺上地砖,这套住宅的建筑平面图(由多个长方形组成)如图所示(图中长度单位:![]() ),请据图解答下列问题.
),请据图解答下列问题.
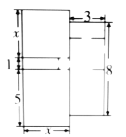
(1)用含![]() 的代数式表示这所住宅的总面积;
的代数式表示这所住宅的总面积;
(2)某公司地砖报价为每平米200元,若![]() ,在现有条件下,王叔叔是否会选择该公司铺地砖?请说明理由.
,在现有条件下,王叔叔是否会选择该公司铺地砖?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组数中,以a、b、c为边长的三角形不是直角三角形的是( )
A. a=3,b=4,c=5B. a=5,b=12,c=13
C. a=1,b=2,c=![]() D. a=
D. a=![]() ,b=2,c=3
,b=2,c=3
查看答案和解析>>
科目:初中数学 来源: 题型:
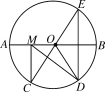
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
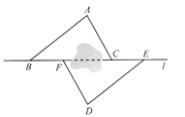
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
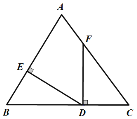
【题目】如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
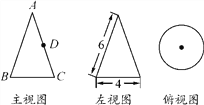
【题目】如图所示是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体上的点B出发,沿表面爬到AC的中点D,请你求出这条路线的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
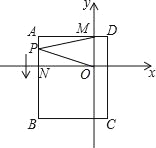
【题目】如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(﹣4,2)、(1,﹣4),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)求B、D两点坐标和长方形ABCD的面积;
(2)一动点P从A出发(不与A点重合),以![]() 个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
(3)是否存在某一时刻t,使三角形AMP的面积等于长方形面积的![]() ?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com