
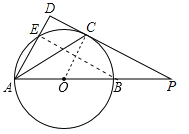
【题目】如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.

(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若tan∠P=![]() ,AD=6,求线段AE的长.
,AD=6,求线段AE的长.
【答案】(1)PC是⊙O的切线;(2)![]()
【解析】试题分析:(1)结论:PC是⊙O的切线.只要证明OC∥AD,推出∠OCP=∠D=90°,即可.
(2)由OC∥AD,推出![]() ,即
,即![]() ,解得r=
,解得r=![]() ,由BE∥PD,AE=ABsin∠ABE=ABsin∠P,由此计算即可.
,由BE∥PD,AE=ABsin∠ABE=ABsin∠P,由此计算即可.
试题解析:解:(1)结论:PC是⊙O的切线.理由如下:
连接OC.∵AC平分∠EAB,∴∠EAC=∠CAB.又∵∠CAB=∠ACO,∴∠EAC=∠OCA,∴OC∥AD.∵AD⊥PD,∴∠OCP=∠D=90°,∴PC是⊙O的切线.
(2)连接BE.在Rt△ADP中,∠ADP=90°,AD=6,tan∠P=![]() ,∴PD=8,AP=10,设半径为r.∵OC∥AD,∴
,∴PD=8,AP=10,设半径为r.∵OC∥AD,∴![]() ,即
,即![]() ,解得r=
,解得r=![]() .∵AB是直径,∴∠AEB=∠D=90°,∴BE∥PD,∴AE=ABsin∠ABE=ABsin∠P=
.∵AB是直径,∴∠AEB=∠D=90°,∴BE∥PD,∴AE=ABsin∠ABE=ABsin∠P=![]() ×
×![]() =
=![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
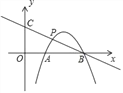
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C.
(1)求抛物线y=﹣x2+ax+b的解析式;
(2)当点P是线段BC的中点时,求点P的坐标;
(3)在(2)的条件下,求sin∠OCB的值.
【答案】(1) y=﹣x2+4x﹣3;(2) 点P的坐标为(![]() ,
,![]() );(3)
);(3) ![]() .
.
【解析】分析:(1)将点A、B代入抛物线y=-x2+ax+b,解得a,b可得解析式;
(2)由C点横坐标为0可得P点横坐标,将P点横坐标代入(1)中抛物线解析式,易得P点坐标;
(3)由P点的坐标可得C点坐标,A、B、C的坐标,利用勾股定理可得BC长,利用sin∠OCB=![]() 可得结果.
可得结果.
详解:(1)将点A、B代入抛物线y=﹣x2+ax+b可得,
![]() ,
,
解得,a=4,b=﹣3,
∴抛物线的解析式为:y=﹣x2+4x﹣3;
(2)∵点C在y轴上,
所以C点横坐标x=0,
∵点P是线段BC的中点,
∴点P横坐标xP=![]() =
=![]() ,
,
∵点P在抛物线y=﹣x2+4x﹣3上,
∴yP=![]()
![]() ﹣3=
﹣3=![]() ,
,
∴点P的坐标为(![]() ,
,![]() );
);
(3)∵点P的坐标为(![]() ,
,![]() ),点P是线段BC的中点,
),点P是线段BC的中点,
∴点C的纵坐标为2×![]() ﹣0=
﹣0=![]() ,
,
∴点C的坐标为(0,![]() ),
),
∴BC=![]() =
=![]() ,
,
∴sin∠OCB=![]() =
=![]() =
=![]() .
.
点睛:本题主要考查了待定系数法求二次函数解析式,二次函数图像与性质,解直角三角形,勾股定理,利用中点求得点P的坐标是解答此题的关键.
【题型】解答题
【结束】
24
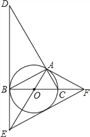
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
(1)求证:△ACF∽△DAE;
(2)若S△AOC=![]() ,求DE的长;
,求DE的长;
(3)连接EF,求证:EF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为20cm2,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…依此类推,则平行四边形AO4C5B的面积为( )

A. ![]() cm2 B.
cm2 B. ![]() cm2 C.
cm2 C. ![]() cm2 D.
cm2 D. ![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BD,CD⊥BD,∠A与∠AEF互补,以下是证明CD//EF的推理过程及理由,请你在横线上补充适当条件,完整其推理过程或理由。
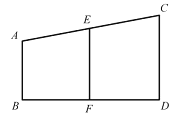
证明:∵AB⊥BD,CD⊥BD(已知)
∴∠ABD=∠CDB=_______________.(____________________)
∴∠ABD+∠CDB=180°
∴AB∥____________(____________________)
又∠A与∠AEF互补(____________________)
∴∠A+∠AEF=___________(____________________)
∴AB//___________(____________________)
∴CD//EF(____________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
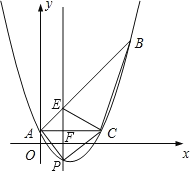
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点。
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点。
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E.F,当四边形AECP的面积最大时,求点P的坐标和四边形AECP的最大面积;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C.P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com