
【题目】如图,在平面直角坐标系中,点 A(0,4)在 y 轴上,点 B(b,0)是 x 轴上一动点,且 4< b <4,△ABC 是以 AB 为直角边,B 为直角顶点的等腰直角三角形.
(1)求点 C 的坐标(用含 b 的式子表示);
(2)以 x 轴为对称轴,作点 C 的对称点 C 连接 BC、AC,请把图形补充完整,并求出△ABC的面积(用含 b 的式子表示);
(3)点 B 在运动过程中, OAC 的度数是否发生变化,若变化请说明理由;若不变化,请直接 写出 OAC 的度数.

【答案】(1)点![]() ;(2)
;(2)![]() ;(3)不变化,
;(3)不变化,![]() .
.
【解析】
(1)过点C作CE⊥x轴,垂足为E,由题意可证△ABO≌△BCE,可得BE=OA=4,BO=EC=-b,则OE=4+b,即求点C的坐标;
(2)根据题意补全图形,根据S△ABC'=S△ABO+S梯形AOEC'-S△BEC'=![]() ×(-b)×4+
×(-b)×4+![]() ×(4-b)(4+b)-
×(4-b)(4+b)-![]() ×4×(-b),可求△ABC′的面积;
×4×(-b),可求△ABC′的面积;
(3)过点A作AF⊥EC',垂足为F,可证四边形AOEF是矩形,可得AO=EF=4,OE=AF=4+b,可证AF=C'F=4+b,可得∠FAC'=45°,且∠OAF=90°,可求∠OAC'=45°.
(1)如图,过点C作CE⊥x轴,垂足为E,

∵△ABC是等腰直角三角形,
∴AB=BC,∠ABC=90°,
∵∠ABE+∠CBE=90°,∠CBE+∠BCE=90°,
∴∠ABE=∠BCE,且AB=BC,∠AOB=∠BEC=90°,
∴△ABO≌△BCE(AAS)
∴BO=CE,AO=BE,
∵点A(0,4),点B(b,0),且-4<b<0,
∴BE=OA=4,BO=EC=-b,
∴OE=4+b
∴点C坐标(4+b,b)
(2)根据题意画出图形,如下图,

∵点C与点C'关于x轴对称,
∴点C'(4+b,-b),C'C⊥x轴,
∵S△ABC'=S△ABO+S梯形AOEC'-S△BEC'=![]() ×(-b)×4+
×(-b)×4+![]() ×(4-b)(4+b)-
×(4-b)(4+b)-![]() ×4×(-b),
×4×(-b),
∴S△ABC'=8-![]() b2,
b2,
(3)点B在运动过程中,∠OAC′的度数不发生变化,
理由如下:如图,过点A作AF⊥EC',垂足为F,

∵AF⊥EC',EC'⊥BE,AO⊥OE,
∴四边形AOEF是矩形,
∴AO=EF=4,OE=AF=4+b,
∵C'F=EF-EC'=4-(-b)=4+b,
∴AF=C'F,且∠AFE=90°,
∴∠FAC'=45°,且∠OAF=90°,
∴∠OAC'=45°


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是( )
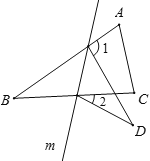
A. 32° B. 64° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线BC//ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形ABC中,∠C=90°,AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,AD、BE相交于点F,过点D作DG∥AB,过点B作BG⊥DG交DG于点G.下列结论:①∠AFB=135°;②∠BDG=2∠CBE;③BC平分∠ABG;④∠BEC=∠FBG.其中正确的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠ABC=3∠C,∠BAC的平分线AD交BC于D,BE⊥AD于E.
(1)如图l,求证:AC﹣AB=2BE.
(2)如图2,将∠DCA沿直线AC翻折,交BA的延长线于点M,连接MD交AC于点N;MA=BA,BE=1,AB=![]() ,求AN的长.
,求AN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点
A(0,4),点B是![]() 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图:在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形.按要求画出下列图形:
(1)将△ABC向右平移5个单位得到△A′B′C′;
(2)将△A′B′C′绕点A′顺时针旋转90°得到△A′DE;
(3)连结EC′,则△A′EC′是 三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC绕点A逆时针方向旋转得到△ADE,其中∠B=50°,∠C=60°.
(1)若AD平分∠BAC时,求∠BAD的度数.
(2)若AC⊥DE时,AC与DE交于点F,求旋转角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:
①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.
其中说法正确的有_________(把你认为说法正确的序号都填上).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com