
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
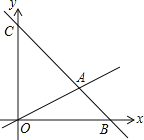
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.
【答案】(1)y=﹣x+6;(2)12;(3)M1(1,![]() )或M2(1,5).
)或M2(1,5).
【解析】
试题分析:(1)利用待定系数法即可求得函数的解析式;
(2)求得C的坐标,即OC的长,利用三角形的面积公式即可求解;
(3)当△OMC的面积是△OAC的面积的![]() 时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
解:(1)设直线AB的解析式是y=kx+b,
根据题意得:![]() ,
,
解得:![]() ,
,
则直线的解析式是:y=﹣x+6;
(2)在y=﹣x+6中,令x=0,解得:y=6,
S△OAC=![]() ×6×4=12;
×6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m=![]() ,
,
则直线的解析式是:y=![]() x,
x,
∵当△OMC的面积是△OAC的面积的![]() 时,
时,
∴M的横坐标是![]() ×4=1,
×4=1,
在y=![]() x中,当x=1时,y=
x中,当x=1时,y=![]() ,则M的坐标是(1,
,则M的坐标是(1,![]() );
);
在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:M1(1,![]() )或M2(1,5).
)或M2(1,5).


科目:初中数学 来源: 题型:
【题目】七年级学生完成课题学习“从数据谈节水”后,积极践行“节约用水,从我做起”,现在从七年级400名学生中选出10名学生统计各自家庭一个月的节水情况如下表:
节水量(m3) | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 |
家庭数 | 1 | 2 | 2 | 4 | 1 |
那么这组数据的众数和平均数分别是( )
A. 0.4m3和0.34m3 B. 0.4m3和0.3m3 C. 0.25m3和0.34m3 D. 0.25m3和0.3m3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料解决问题:
材料:古希腊著名数学家 毕达哥拉斯发现把数1,3,6,10,15,21…这些数量的(石子),都可以排成三角形,则称像这样的数为三角形数.
把数 1,3,6,10,15,21…换一种方式排列,即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看,把1,3,6,10,15,…叫做三角形数“名副其实”.
(1)设第一个三角形数为a1=1,第二个三角形数为a2=3,第三个三角形数为a3=6,请直接写出第n个三角形数为an的表达式(其中n为正整数).
(2)根据(1)的结论判断66是三角形数吗?若是请说出66是第几个三角形数?若不是请说明理由.
(3)根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96
B.69
C.66
D.99
查看答案和解析>>
科目:初中数学 来源: 题型:
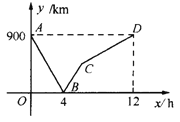
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
信息读取:(1)甲、乙两地之间的距离为
(2)请解释图中点B的实际意义;
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同,在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某一平地上,有一棵树高8米的大树,一棵树高3米的小树,两树之间相距12米。今一只小鸟在其中一棵树的树梢上,要飞到另一棵树的树梢上,问它飞行的最短距离是多少?(画出草图然后解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中,计算正确的是( )
A. (a﹣b)2=a2﹣b2 B. (2x﹣y)2=4x2﹣2xy+y2
C. (a﹣3b)(a+3b)=a2﹣9b2 D. (15 x2 y-10x y2) ÷5xy=3x-2 y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动. 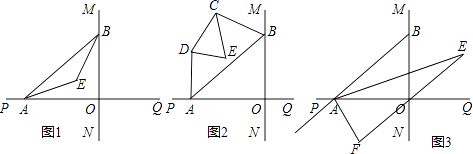
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A,B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A,B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E,F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com