
【题目】如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ= ![]() ,那么当点P运动一周时,点Q运动的总路程为 .
,那么当点P运动一周时,点Q运动的总路程为 . 
【答案】4
【解析】解:在Rt△AOB中,∵∠ABO=30°,AO=1,∴AB=2,BO= ![]() =
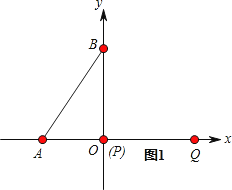
= ![]() ,①当点P从O→B时,如图1、图2所示,点Q运动的路程为
,①当点P从O→B时,如图1、图2所示,点Q运动的路程为 ![]() ,
,
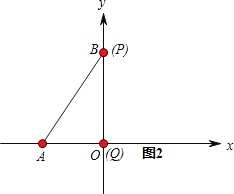
②当点P从B→C时,如图3所示,这时QC⊥AB,则∠ACQ=90°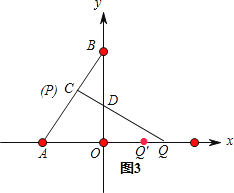
∵∠ABO=30°
∴∠BAO=60°
∴∠OQD=90°﹣60°=30°
∴cos30°= ![]() ∴AQ=
∴AQ= ![]() =2
=2
∴OQ=2﹣1=1
则点Q运动的路程为QO=1,
③当点P从C→A时,如图3所示,点Q运动的路程为QQ′=2﹣ ![]() ,
,
④当点P从A→O时,点Q运动的路程为AO=1,
∴点Q运动的总路程为: ![]() +1+2﹣
+1+2﹣ ![]() +1=4
+1=4
故答案为:4
本题主要是应用三角函数定义来解直角三角形,此题的解题关键是理解题意,正确画出图形;线段的两个端点看成是两个动点,将线段移动问题转化为点移动问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2 , 从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2 .
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:
指数运算 | 21=2 | 22=4 | 23=8 | … | 31=3 | 32=9 | 33=27 | … |
新运算 | log22=1 | log24=2 | log28=3 | … | log33=1 | log39=2 | log327=3 | … |
根据上表规律,某同学写出了三个式子:①log216=4,②log525=5,③log2 ![]() =﹣1.其中正确的是( )
=﹣1.其中正确的是( )
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC= ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=120°,AB=AC=6.P是底边BC上的一个动点(P与B、C不重合),以P为圆心,PB为半径的⊙P与射线BA交于点D,射线PD交射线CA于点E. 
(1)若点E在线段CA的延长线上,设BP=x,AE=y,求y关于x的函数关系式,并写出x的取值范围.
(2)当BP=2 ![]() 时,试说明射线CA与⊙P是否相切.
时,试说明射线CA与⊙P是否相切.
(3)连接PA,若S△APE= ![]() S△ABC , 求BP的长.
S△ABC , 求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的平均数,中位数分别是( ) 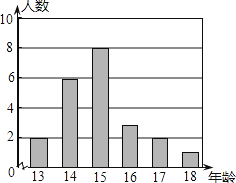
A.15.5,15.5
B.15.5,15
C.15,15.5
D.15,15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为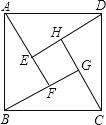
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com