
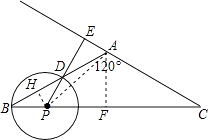
【题目】如图,△ABC中,∠BAC=120°,AB=AC=6.P是底边BC上的一个动点(P与B、C不重合),以P为圆心,PB为半径的⊙P与射线BA交于点D,射线PD交射线CA于点E. 
(1)若点E在线段CA的延长线上,设BP=x,AE=y,求y关于x的函数关系式,并写出x的取值范围.
(2)当BP=2 ![]() 时,试说明射线CA与⊙P是否相切.
时,试说明射线CA与⊙P是否相切.
(3)连接PA,若S△APE= ![]() S△ABC , 求BP的长.
S△ABC , 求BP的长.
【答案】
(1)解:过A作AF⊥BC于F,过P作PH⊥AB于H,
∵∠BAC=120°,AB=AC=6,
∴∠B=∠C=30°,
∵PB=PD,
∴∠PDB=∠B=30°,CF=ACcos30°=6× ![]() =3
=3 ![]() ,
,
∴∠ADE=30°,
∴∠DAE=∠CPE=60°,
∴∠CEP=90°,
∴CE=AC+AE=6+y,
∴PC= ![]() =
= ![]() ,
,
∵BC=6 ![]() ,
,
∴PB+CP=x+ ![]() =6
=6 ![]() ,
,
∴y=﹣ ![]() x+3,
x+3,
∵BD=2BH= ![]() x<6,
x<6,
∴x<2 ![]() ,
,
∴x的取值范围是0<x<2 ![]()
(2)解:∵BP=2 ![]() ,∴CP=4
,∴CP=4 ![]() ,
,
∴PE= ![]() PC=2
PC=2 ![]() =PB,
=PB,
∴射线CA与⊙P相切
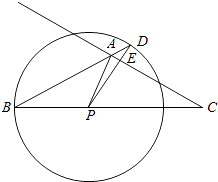
(3)解:当D点在线段BA上时,
连接AP,
∵S△ABC= ![]() BCAF=
BCAF= ![]() ×6
×6 ![]() ×3=9
×3=9 ![]() ,
,
∵S△APE= ![]() AEPE=
AEPE= ![]() y
y ![]() ×(6+y)=
×(6+y)= ![]() S△ABC=
S△ABC= ![]() ,
,
解得:y= ![]() ,代入y=﹣
,代入y=﹣ ![]() x+3得x=4
x+3得x=4 ![]() ﹣
﹣ ![]() .
.
当D点BA延长线上时,
PC= ![]() EC=
EC= ![]() (6﹣y),
(6﹣y),
∴PB+CP=x+ ![]() (6﹣y)=6
(6﹣y)=6 ![]() ,
,
∴y= ![]() x﹣3,
x﹣3,
∵∠PEC=90°,
∴PE= ![]() =
= ![]() =
= ![]() (6﹣y),
(6﹣y),
∴S△APE= ![]() AEPE=
AEPE= ![]() x=
x= ![]() y
y ![]() (6﹣y)=
(6﹣y)= ![]() S△ABC=
S△ABC= ![]() ,
,
解得y= ![]() 或
或 ![]() ,代入y=
,代入y= ![]() x﹣3得x=3
x﹣3得x=3 ![]() 或5
或5 ![]() .
.
综上可得,BP的长为4 ![]() ﹣
﹣ ![]() 或3
或3 ![]() 或5
或5 ![]() .
.
【解析】(1)过A作AF⊥BC于F,过P作PH⊥AB于H,根据等腰三角形的性质得到CF=ACcos30°=6× ![]() =3
=3 ![]() ,推出∠CEP=90°,求得CE=AC+AE=6+y,列方程PB+CP=x+
,推出∠CEP=90°,求得CE=AC+AE=6+y,列方程PB+CP=x+ ![]() =6
=6 ![]() ,于是得到y=﹣
,于是得到y=﹣ ![]() x+3,根据BD=2BH=
x+3,根据BD=2BH= ![]() x<6,即可得到结论;(2)根据已知条件得到PE=
x<6,即可得到结论;(2)根据已知条件得到PE= ![]() PC=2
PC=2 ![]() =PB,于是得到射线CA与⊙P相切;(3)D在线段BA上和延长线上两种情况,根据三角形的面积列方程即可得到结果.本题考查了直线与圆的位置关系,等腰三角形的性质,直角三角形的性质,三角形面积的计算,求一次函数的解析式,证得PE⊥AC是解题的关键.
=PB,于是得到射线CA与⊙P相切;(3)D在线段BA上和延长线上两种情况,根据三角形的面积列方程即可得到结果.本题考查了直线与圆的位置关系,等腰三角形的性质,直角三角形的性质,三角形面积的计算,求一次函数的解析式,证得PE⊥AC是解题的关键.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )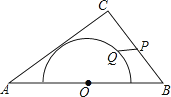
A.6
B.2 ![]() +1
+1
C.9
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ= ![]() ,那么当点P运动一周时,点Q运动的总路程为 .
,那么当点P运动一周时,点Q运动的总路程为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形的两边长分别为m+3,m+13;如图2的长方形的两边长分别为m+5,m+7.(其中m为正整数)

(1)写出两个长方形的面积S1,S2,并比较S1,S2的大小;
(2)现有一个正方形的周长与图1中的长方形的周长相等.试探究该正方形的面积与长方形的面积的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由.
(3)在(1)的条件下,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有19个,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是 .
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是 .
(3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺序通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
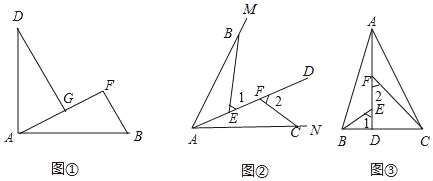
【题目】(1)感知:如图①.AB=AD,AB⊥AD,BF⊥AF于点F,DG⊥AF于点G.求证:△ADG≌△BAF;
(2)拓展:如图②,点B,C在∠MAN的边AM,AN上,点E,F在∠MAN在内部的射线AD上,∠1,∠2分别是△ABE,△CAF的外角,已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)应用:如图③,在△ABC中,AB=AC,AB>BC,点在D边BC上,CD=2BD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为12,则△ABE与△CDF的面积之和为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com