[题目]下列算式① =±3,② =9,③26÷23=4,④ =2016,⑤a+a=a2 ．运算结果正确的概率是( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

【题目】下列算式
① =±3；② =9；③26÷23=4；④ =2016；⑤a+a=a2 ．
运算结果正确的概率是（　　）
A.
B.
C.
D.

【答案】B
【解析】解：① =3，故此选项错误；
② = =9，正确；
③26÷23=23=8，故此选项错误；
④ =2016，正确；
⑤a+a=2a，故此选项错误，
故运算结果正确的概率是：．
故选：B．
【考点精析】利用实数的运算和概率公式对题目进行判断即可得到答案，需要熟知先算乘方、开方，再算乘除，最后算加减，如果有括号，先算括号里面的，若没有括号，在同一级运算中，要从左到右进行运算；一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，事件A包含其中的m中结果，那么事件A发生的概率为P（A）=m/n．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示，请在网格中涂出一种该几何体的主视图，且使该主视图是轴对称图形．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为（　　）

A.1
B.2
C.3
D.4

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知正方形ABCD的边长为1，点P为正方形内一动点，若点M在AB上，且满足△PBC∽△PAM，延长BP交AD于点N，连结CM．

（1）如图一，若点M在线段AB上，求证：AP⊥BN；AM=AN；
（2）①如图二，在点P运动过程中，满足△PBC∽△PAM的点M在AB的延长线上时，AP⊥BN和AM=AN是否成立？（不需说明理由）
②是否存在满足条件的点P，使得PC= ？请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，△ABC中，∠BAC=120°，AB=AC=6．P是底边BC上的一个动点（P与B、C不重合），以P为圆心，PB为半径的⊙P与射线BA交于点D，射线PD交射线CA于点E．

（1）若点E在线段CA的延长线上，设BP=x，AE=y，求y关于x的函数关系式，并写出x的取值范围．
（2）当BP=2 时，试说明射线CA与⊙P是否相切．
（3）连接PA，若S△APE= S△ABC ，求BP的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5．将三张牌背面朝上，洗匀后放在桌子上．
（1）甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．请用列表法或画树状图的方法，求两人抽取相同数字的概率；
（2）若两人抽取的数字和为2的倍数，则甲获胜；若抽取的数字和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某校男子足球队的年龄分布如图所示，则根据图中信息可知这些队员年龄的平均数，中位数分别是（　　）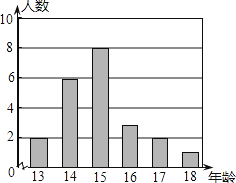
A.15.5，15.5
B.15.5，15
C.15，15.5
D.15，15